index.html

Tensorial Tutorials

Common Tensor Operations With an Oblique Coordinate System

David Park

The notebook must be evaluated in order as later sections depend upon results established in earlier sections.

In this notebook we show how to:
1) Represent and manipulate various objects in an oblique coordinate system.
2) Use full tensor notation with a tensor basis and CircleTimes.
3) Evaluate expressions such as T[u,v] where T is a tensor and u and v are vectors.
4) Write transformations between coordinate systems.

Initialization

In[6]:=

We define tensor shortcuts and index flavors for the various tensors that will be used in the notebook.

In[7]:=

In[8]:=

1. Basis Vectors and Reciprocal Basis

We establish the natural and dual basis vectors for a Cartesian coordinate system. Notice that a first order tensor g can be given vector components.

In[11]:=

Out[13]=

${g_1^1→ {1, 0, 0}, g_2^2→ {0, 1, 0}, g_3^3→ {0, 0, 1}, g_1^1→ {1, 0, 0}, g_2^2→ {0, 1, 0}, g_3^3→ {0, 0, 1}}$

We will represent tensors in the oblique frame by red indices. The rows of the GBasis matrix will be the oblique basis vectors. The following establishes the oblique basis as tensor objects.

In[14]:=

Out[16]=

There is an easy way to calculate the red reciprocal basis vectors. Just take the rows of Transpose[Inverse[GBasis]]. However, let's work by more formal tensor methods. This gives us some practice in performing tensor manipulations with Tensorial and Mathematica. We first usurp guu[red@i,red@j] to represent the components of gu[i]. (We will later use it to represent the metric tensor.)

In[17]:=

Out[19]=

Out[21]=

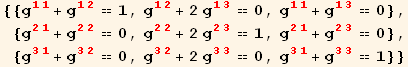
Out[23]=

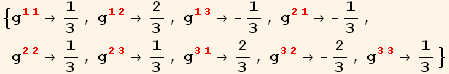
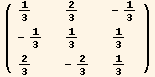
Out[25]//MatrixForm=

( {{1/3, 2/3, -1/3}, {-1/3, 1/3, 1/3}, {2/3, -2/3, 1/3}} )

Out[27]=

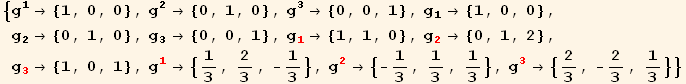
We now have the basis and reciprocal basis vectors in both the black (Cartesian) and red (oblique) coordinate system.

We can check that we have obtained a proper solution for the reciprocal basis.

In[28]:=

Out[28]=

Out[29]//MatrixForm=

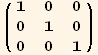
( {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}} )

Notice how convenient and powerful the ToArrayValues command is.

2. Calculating the Metric

We can calculate the metric in the red coordinates by the standard definition. (The metric in the black coordinates is just the IdentityMatrix.)

In[30]:=

Out[30]=

Out[31]//MatrixForm=

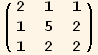
( {{2, 1, 1}, {1, 5, 2}, {1, 2, 2}} )

We set the metric values using SetTensorValueRules. We want to set both the down and up version of the metric. For no other reason than to illustrate the difference, we will set the Cartesian metric values using SetTensorValues.

In[32]:=

We could also have done this a little more compactly with...

In[36]:=

Notice again that we are using g with one index and g with two indices. They are different objects and do not interfer with each other.

In[38]:=

Out[38]=

What happened to the Cartesian metric values? They are stored as UpValues of g.

In[39]:=

Out[39]=

The following illustrates how definitions are immediately applied, but the substitution rules are only applied when specified. Using substitution rules is nice for learning tensor calculus and Tensorial. We can more clearly control and see the explicit steps.

In[40]:=

Out[40]=

${g_ (ij)^(ij), g_ (ij)^(ij)}$

Out[41]=

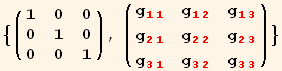
${( {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}} ), ( {{g_ (11)^(11), g_ (12)^(12), g_ (13)^(13)}, {g_ (21)^(21), g_ (22)^(22), g_ (23)^(23)}, {g_ (31)^(31), g_ (32)^(32), g_ (33)^(33)}} )}$

Out[42]=

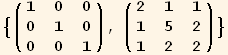
{( {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}} ), ( {{2, 1, 1}, {1, 5, 2}, {1, 2, 2}} )}

One the other hand, ToArrayValues automatically uses not only value definitions, but also uses value rules.

In[43]:=

Out[43]=

${g_ (ij)^(ij), g_ (ij)^(ij)}$

Out[44]=

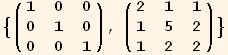
{( {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}} ), ( {{2, 1, 1}, {1, 5, 2}, {1, 2, 2}} )}

3. Dot Product of Two Vectors in the Two Coordinate Systems

Here are two vectors in the black coordinate system. In the natural Cartesian basis the up and down components of the vectors are the same.

In[45]:=

Out[49]=

${u_1^1→2, u_2^2→ -1, u_3^3→3, u_1^1→2, u_2^2→ -1, u_3^3→3, v_1^1→1, v_2^2→1, v_3^3→2, v_1^1→1, v_2^2→1, v_3^3→2}$

The tensor method of taking their dot product is...

In[50]:=

Out[50]=

Out[51]=

To compute the up components of u in the red frame we use the standard definition. We need to set IndexParsingRules because Tensorial does not know how to extract indices from a dot product with one factor an array. The index parsing rule extracts the tensor component of the dot product.

In[52]:=

$IndexParsingRules = {a_List . b_→b} ;$

Out[54]=

Out[56]=

Out[58]=

Out[60]=

Out[61]=

$3 {0, 0, 1} . g_i^i - {0, 1, 0} . g_i^i + 2 {1, 0, 0} . g_i^i$

Out[62]=

We can calculate the down values by lowering the index.

In[64]:=

Out[64]=

Out[65]=

Out[67]=

${u_1^1→2, u_2^2→ -1, u_3^3→3, u_1^1→2, u_2^2→ -1, u_3^3→3, u_1^1→ -1, u_2^2→0, u_3^3→3, u_1^1→1, u_2^2→5, u_3^3→5}$

All of these different u components represent the same geometric object. Now, let's calculate the components of v in the red frame. Just for variety we will calculate the down components of the v vector first and then raise the index to obtain the up values.

In[68]:=

Out[68]=

Out[69]=

Out[70]=

Out[71]=

In[73]:=

Out[73]=

Out[74]=

Out[76]=

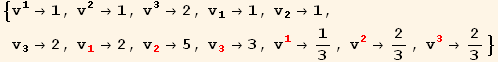
${v_1^1→1, v_2^2→1, v_3^3→2, v_1^1→1, v_2^2→1, v_3^3→2, v_1^1→2, v_2^2→5, v_3^3→3, v_1^1→1/3, v_2^2→2/3, v_3^3→2/3}$

We can calculate the dot product by 4 different methods in each of the coordinate systems. We should and do obtain the same answer by all methods.

In[77]:=

Out[78]=

${u_i^i v_i^i, u_i^i v_i^i, g_ (ij)^(ij) u_i^i v_j^j, g_ (ij)^(ij) u_i^i v_j^j, u_i^i v_i^i, u_i^i v_i^i, g_ (ij)^(ij) u_i^i v_j^j, g_ (ij)^(ij) u_i^i v_j^j}$

Out[79]=

4. A Second Order Tensor T Evaluated on Two Vectors
Working with Tensor Bases

Suppose we have a second order tensor T with the following components in the standard Cartesian frame.

In[80]:=

Out[82]=

Let's evaluate this tensor operating on the u and v vectors defined in Section 3. We can evaluate T on the two vectors by two methods. So far, we have only the up components of T but all components of the metric g and the vectors u and v.

In[83]:=

Out[83]=

${T_ (ij)^(ij) u_i^i v_j^j, g_ (im)^(im) g_ (jn)^(jn) T_ (mn)^(mn) u_i^i v_j^j}$

Out[84]=

Let's be more formal and write out T explicitly in terms of the second order basis tensors, which are...

In[85]:=

Out[85]=

${g_1^1⊗g_1^1, g_1^1⊗g_2^2, g_1^1⊗g_3^3, g_2^2⊗g_1^1, g_2^2⊗g_2^2, g_2^2⊗g_3^3, g_3^3⊗g_1^1, g_3^3⊗g_2^2, g_3^3⊗g_3^3}$

The multiplication symbol is CircleTimes. It can be entered [ESC]c*[ESC] or by typing "\[ " followed by "CircleTimes]". I have it on a palette. It is also on the General Operators subpalette in the CompleteCharacters palette. This type of expression is sometimes called a dyad.

So the tensor can be represented as...

In[86]:=

Out[86]=

Out[87]=

Out[88]=

Out[89]=

We call this the basis form of a tensor.

The following cell evaluates T on u and v using the full basis of the tensor.

In[90]:=

$%%//PushOnto[{CircleTimes[__]}]$

Out[91]=

Out[93]=

Out[95]=

Out[97]=

Out[99]=

Out[101]=

Out[103]=

Providing we have the down components of u and v we could also evaluate in one less step using EvaluateDotProducts.

In[104]:=

$%%//PushOnto[{CircleTimes[__]}]$

Out[105]=

Out[107]=

Out[109]=

Out[111]=

Out[113]=

Out[115]=

With Tensorial, we can concentrate on the basic definitions and operations. All the tedious calculations, plug and chug as in the last step above, can be relegated to the computer.

5. T Components in Oblique Coordinates

Using Basic Definitions

Now, let's calculate and store the components of T in oblique coordinates. We start with the standard definition for calculating the components.

In[116]:=

Out[118]=

Out[120]=

Out[122]=

Out[124]=

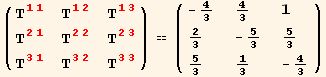
Out[126]=

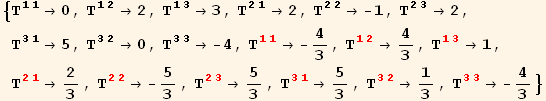
Since we have previously calculated the components of u, v and g in the red frame, we can now evaluate T[u,v] completely in the red frame. We should obtain the same answer as in the black frame.

In[127]:=

Out[127]=

Out[128]=

We could calculate the red frame components of T for other index configurations by the same method as above. Just put the desired combination or red basis or reciprocal basis vectors in the slots. But, since we have one set of components in the red frame, we can calculate the other index configurations simply by lowering indices with the metric tensor. For example...

In[129]:=

Out[129]=

Out[130]=

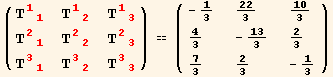
As Linear Transformations

There is another and perhaps more conventional method for calculating the components in the red frame. In Section 1, we simply gave the red basis vectors. But instead, we could have considered them to have been obtained as a linear transformation of the natural Cartesian basis vectors. We can represent this linear transformation by...

In[131]:=

Out[131]=

We will always write the transformation matrices with the indices going northwest to southeast, that is, in the up-down configuration, Aud. The two indices correspond to different coordinate systems. The indices will always have different flavors. It turns out that the components of Aud will be given by the transpose of the GBasis matrix of Section 1, so let's set them and check them.

In[132]:=

Out[133]=

In[134]:=

Out[134]=

Out[135]=

To write the transformation going from one frame to another, we put in an A matrix for each index to be transformed and line up the colors. We have to be careful how the A tensor is initially defined. As a matrix equation we would obtain the obliqe basis by GBasis.(Euclidean basis vectors). But if we look at the first equation above, we really have the transpose when g is written on the right. The k summation indicies are not adjacent. This tells us that A must be the transpose of GBasis.

To obtain the transformation going the other way we need the inverse of A. This corresponds to simply switching the colors of the first and second slots of A. But we must actually calculate and set the values.

In[136]:=

Out[137]=

Here is the inverse transformation...

In[138]:=

Out[138]=

Out[139]=

We will generally need both forms of the transformation matrix. One form will be used to transform down indices and the other form will be used to transform up indices. Let's see how we use them to transform the T matrix from the black to the red frame. Just line up the colors of the indices, with summations on the "old" components. This checks with our previous calculation.

In[140]:=

Out[140]=

Out[141]=

We can then obtain the other index configurations by lowering indices.

Previously we calculated the up and down components of u in the red frame.

In[142]:=

Out[142]=

${u_1^1→2, u_2^2→ -1, u_3^3→3, u_1^1→2, u_2^2→ -1, u_3^3→3, u_1^1→ -1, u_2^2→0, u_3^3→3, u_1^1→1, u_2^2→5, u_3^3→5}$

Let's calculate the down components of u in the black frame starting from the red frame.

In[143]:=

Out[143]=

Out[144]=

Since the black frame has the natural Cartesian basis vectors, the down components should be the same as the up components. The following is not a proper tensor equation and if we try to use ToArrayValues on the entire equation we will obtain error messages because the free indices do not agree. But, if we map ToArrayValues to each side of the equation, the calculation will work.

In[145]:=

Out[145]=

Out[146]=

Eliminate the index parsing rule

In[147]:=

Created by Mathematica (November 22, 2007)