2.   The Strain Tensor

Initial rules and definitions (Automatically Initialized)

Using special characters :
It is convenient to specify important and frequently used tensors like basis vectors, metric tensors, strain,.. to use special characters. However, it may be tedious to have to go to the palette "CompleteCharacters" or to "Copy and Paste" each time we need such a character. Then the solution is to define in the shortcuts an simple alias for each notation ( like bv1 for e ).

Black, Red or Blue Basis

We consider a body with a system of coordinates attached permanently to each point of it. So these coordinates are conserved during the deformation of the body. These coordinates are called particle coordinates or convected coordinates.
A line element of a given body before deformation in the red basis is given by :

or with the short notation :

with the square of its length :

After deformation, the line element dâ connecting the same material points is different in length and direction and may be written, where {} are the vectors into which the original basis {} is deformed

The deformation is then characterized by  the quantities

Question : is a tensor ? To check this we have to perfom a basis change. We write da and dâ in a new "blue" basis.

Of course the basis change is common to both systems e and ê because we are using convected coordinates (there are no difference between and ):

Therefore by the basis change , transforms like a tensor.

The Strain Tensor (γ or E)

The strain tensor is defined by    =-
which corresponds to the degree of deformation :  (dâ.dâ – da.da) =

The strain is a symmetric tensor like the metric.

Now, we want to calculate the strain tensor from the covariant components of the metric tensor :

Using the fact that =   is a Kronecker δ , we can calculate . From the definitions of and ,

Neglecting the second order term    :

Both γ and ζ are tensors, so that we have the relation :

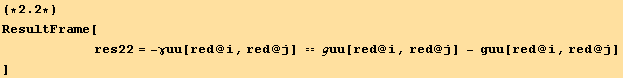
The deformation tensor is completely described when, for each point s of the body, we know the displacement vector u, which extend from the position before deformation to that occupied by the same material point after deformation.

The displacement can be written :

To simplify the problem in a first approch, we consider rectilinear coordinate systems , in which the basis vectors are constant  (and for that we define ConstantBasisRules[e_])

Now using the definition of the strain tensor = dâ.dâ –  da.da = dâu2 – da2

Taking into account that is a constant, this gives

which has the correct i⇔j symmetry ( is symmetrical). The last term which is quadratic in the displacement can be neglected for sufficiently small displacement. Then we have simply

In practice we shall prefer in the following as a measure of the strain the tensor   = /2

Created by Mathematica  (November 27, 2007)