3.   The Cross Product

Initialization

Needs["TensorCalculus4`Tensorial`"]

Needs["TContinuumMechanics2`TContinuumMechanics`"] <br />

numequ = 1 ;

oldflavors = IndexFlavors ;

ClearIndexFlavor/@oldflavors ;

DeclareIndexFlavor[{black, Black}, {red, Red}, {green, ForestGreen}, {star, SuperStar}, {blue, Blue}, {hat, OverHat}, {tilde, OverTilde}, {bar, OverBar}]

DeclareBaseIndices[{1, 2, 3}] ;

{NDim, BaseIndices} ;

DefineTensorShortcuts[{{, u, v, w, dr, ds, dt, dF, γ}, 1}, {{g, β, a, T}, 2}, {{ε, e, T}, 3}] ;

The following values are taken as an example of a (red) basis frame :

SetTensorValues[gdd[i, j], IdentityMatrix[3]]

RedBasisVectors = ({{1, 1, 0}, {0, 1, 2}, {1, 0, 1}}) ; RedMetric = ( {{2, 1, 1}, {1, 5, 2}, {1, 2, 2}} ) ;

SetTensorValueRules[d[red @ i], RedBasisVectors]

SetTensorValueRules[u[red @ i], Inverse[RedBasisVectors//Transpose]]

SetTensorValueRules[gdd[red @ i, red @ j], RedMetric]

SetTensorValueRules[guu[red @ i, red @ j], Inverse[RedMetric]]

Generalities

Completely antisymmetric symbol

Tuuu[i, j, k] εddd[i, j, k]

(%//EinsteinSum[])/.PermutationSymbolRule[ε]

T_ (ijk)^(ijk) ε_ (ijk)^(ijk)

T_ (123)^(123) - T_ (132)^(132) - T_ (213)^(213) + T_ (231)^(231) + T_ (312)^(312) - T_ (321)^(321)

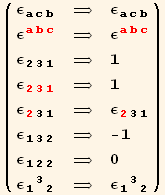
Remark : AntiSymmetric includes the factor 1/ n!

Tuuu[i, j, k]

(%//AntiSymmetric[black/@{i, j, k}])/.{i:→1, j:→2, k:→3}

T_ (ijk)^(ijk)

1/6 (T_ (123)^(123) - T_ (132)^(132) - T_ (213)^(213) + T_ (231)^(231) + T_ (312)^(312) - T_ (321)^(321))

Definition of the operator CrossProductExpansion which calculate the ScalarTripleProduct of the basis set, and the Cross Product of two basis vectors.:
CrossProductExpansion[e_,e_][expr] expand the triple scalar products and the cross products expressed in a given basis e into LeviCivita symbols e. The considered space is three-dimensional.

In an orthonormal (blue-)basis, e_ (i j k)^(i j k) is simply a PermutationSymbol [e] and the cross product of two basis vectors is given by

u[blue @ i] ×u[blue @ j]//CrossProductExpansion[, e, k]//EinsteinSum[]

(%//ArrayExpansion[blue @ i, blue @ j])/.PermutationSymbolRule[e]//MatrixForm

e_ (ij1)^(ij1) _1^1 + e_ (ij2)^(ij2) _2^2 + e_ (ij3)^(ij3) _3^3

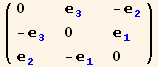
( {{0, _3^3, -_2^2}, {-_3^3, 0, _1^1}, {_2^2, -_1^1, 0}} )

Determinants

The two kinds of PermutationSymbolRule[ε] εddd[i,j,k] or εuuu[i,j,k] also allow to calculate determinants (in the base system) :

detA = ((A = adu[1, i] adu[2, j] adu[3, k] εddd[i, j, k])//EinsteinSum[])/.PermutationSymbolRule[ε] ;

detA1 = ((A1 = adu[i, 1] adu[j, 2] adu[k, 3] εuuu[i, j, k])//EinsteinSum[])/.PermutationSymbolRule[ε] ;

A

A1

detA

detA == detA1

A=. ; A1=.

a_ (1i)^(1i) a_ (2j)^(2j) a_ (3k)^(3k) ε_ (ijk)^(ijk)

a_ (i1)^(i1) a_ (j2)^(j2) a_ (k3)^(k3) ε_ (ijk)^(ijk)

True

and of course we can verify the equivalence of the above detA with the build in Det function :

adu[i, j]//ArrayExpansion[{i, j}]

Det[%] == detA

a_ (ij)^(ij)

Determinants of the metric tensors g

( {{Det[g_ (ij)^(ij)], ⇒, 1/9}, {Det[g_ (ij)^(ij)], ⇒, 9}, {Det[g_ (ij)^(ij)], ⇒, 1}} )

Transformation tensors β

Example : Basis change from the black to the red basis (see Chapter 1)

u[j] . d[red @ i]//EvaluateDotProducts[ , β]

d[red @ i] == d[j] %

%//KroneckerAbsorb[β]

β_ (ji)^(ji)

_i^i == _j^j β_ (ji)^(ji)

True

SetTensorValueRules[βud[j, red @ i], (d[red @ i]//ArrayExpansion[red @ i])/.TensorValueRules[, g]]

Determinants of the transformation tensors β

Introduction of a determinant Δ of a transformation matrix β between the initial flavor, flavor1, to the final flavor, flavor2.
Note : I shall have to check the homogeneity of the notations between initial and final situations (see ToFlavor for instance, for which it is the reverse).

Δ[β_][flavor1_, flavor2_] := Det[βud[flavor1 @ i, flavor2 @ j]//ArrayExpansion[flavor1 @ i]//ArrayExpansion[flavor2 @ j]]

Δ[β][red, blue]

Δ[β][black, red]/.TensorValueRules[β]

3

Introduction of the elementary volume formed by the basis set _ i^i (for the red flavor) associated to g

Tensor[black @ g] == (Tensor[black @ g]//VolumeSquare[black @ g])

Tensor[red @ g] == (Tensor[red @ g]//VolumeSquare[red @ g])

g == 1

g == 9

From the relation between the two basis    g_ (hk)^(hk)= g_ (ij)^(ij) β_ (ih)^(ih)  β_ (ik)^(ik)

ResultFrame[res31 = 1/Δ == flavor @ g^(1/2)]

      1/Δ == flavor[g]^(1/2)       (3.1)

Basis Change of any tensor

Examples :

We can now extend the antisymmetric tensor   ε ddd [ i , j , k ] to general coordinate systems and define a tensor eddd [ i , j , k ] and equivalently a tensor  euuu [ i , j , k ] . These tensors are called permutation tensors or Levi-Civita tensors.

Levi-Civita tensors

eddd[red @ i, red @ j, red @ k]

e_ (ijk)^(ijk)

%//LeviCivitaSimplify[e, ε][g, red]

(Tuuu[i, j, k]//ToFlavor[red, black]) %//EinsteinSum[] ;

%/.PermutationSymbolRule[ε]//Factor

%//VolumeSquare[red @ g]

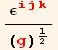
(g)^1/2 ε_ (ijk)^(ijk)

(g)^1/2 (T_ (123)^(123) - T_ (132)^(132) - T_ (213)^(213) + T_ (231)^(231) + T_ (312)^(312) - T_ (321)^(321))

3 (T_ (123)^(123) - T_ (132)^(132) - T_ (213)^(213) + T_ (231)^(231) + T_ (312)^(312) - T_ (321)^(321))

euuu[red @ i, red @ j, red @ k]//LeviCivitaSimplify[e, ε][g, red]

(Tddd[i, j, k]//ToFlavor[red, black]) %//EinsteinSum[] ;

%/.PermutationSymbolRule[ε]//Factor

%//VolumeSquare[red @ g]

ε_ (ijk)^(ijk)/(g)^1/2

(T_ (123)^(123) - T_ (132)^(132) - T_ (213)^(213) + T_ (231)^(231) + T_ (312)^(312) - T_ (321)^(321))/(g)^1/2

1/3 (T_ (123)^(123) - T_ (132)^(132) - T_ (213)^(213) + T_ (231)^(231) + T_ (312)^(312) - T_ (321)^(321))

Cross Product

We also introduce here, to be complete, the standard notation used in the Standard Packages.

<<Calculus`VectorAnalysis`

CrossProduct[{a1, a2, a3}, {b1, b2, b3}]

{-a3 b2 + a2 b3, a3 b1 - a1 b3, -a2 b1 + a1 b2}

We can define for convenience :

coord[flavor_][a_] := a[flavor @ k]//ArrayExpansion[flavor @ k]

CrossProduct[coord[red][uu], coord[red][vu]]

{-u_3^3 v_2^2 + u_2^2 v_3^3, u_3^3 v_1^1 - u_1^1 v_3^3, -u_2^2 v_1^1 + u_1^1 v_2^2}

coord[black][uu]

{u_1^1, u_2^2, u_3^3}

CrossProduct[coord[black][uu], coord[black][vu]]

{-u_3^3 v_2^2 + u_2^2 v_3^3, u_3^3 v_1^1 - u_1^1 v_3^3, -u_2^2 v_1^1 + u_1^1 v_2^2}

eddd[i, j, k] uu[i] vu[j]

(%//EinsteinSum[]//ArrayExpansion[k]//LeviCivitaSimplify[e, ε][g, black])/.PermutationSymbolRule[ε]//Factor

%//VolumeSquare[g]

e_ (ijk)^(ijk) u_i^i v_j^j

eddd[red @ i, red @ j, red @ k] uu[red @ i] vu[red @ j]

(%//EinsteinSum[]//ArrayExpansion[red @ k]//LeviCivitaSimplify[e, ε][g, red])/.PermutationSymbolRule[ε]//Factor

%//VolumeSquare[red @ g]

e_ (ijk)^(ijk) u_i^i v_j^j

{-(g)^1/2 (u_3^3 v_2^2 - u_2^2 v_3^3), (g)^1/2 (u_3^3 v_1^1 - u_1^1 v_3^3), -(g)^1/2 (u_2^2 v_1^1 - u_1^1 v_2^2)}

{-3 (u_3^3 v_2^2 - u_2^2 v_3^3), 3 (u_3^3 v_1^1 - u_1^1 v_3^3), -3 (u_2^2 v_1^1 - u_1^1 v_2^2)}

The "black" basis is orthonormal. But not the red's one  :

Cross[u[red @ 1], u[red @ 2]]    - u[red @ 3]    /.TensorValueRules[]

{-1/3, 2/3, 0}

Consider the three following vectors :

 = uu[i] d[i] ;

 = vu[j] d[j] ;

 = wd[k] u[k] ;

((×) . //ToFlavor[red]//LinearBreakout[Cross][d[_], u[_]])//CrossProductExpansion[, e, h]

%//EvaluateDotProducts[, g, False]

%//MetricSimplify[g]

%//UpDownSwap[red @ k]

(e_ (ijh)^(ijh) u_i^i v_j^j _h^h) . (w_k^k _k^k)

e_ (ijh)^(ijh) g_ (hk)^(hk) u_i^i v_j^j w_k^k

e_ (ijk)^(ijk) u_i^i v_j^j w_k^k

e_ (ijk)^(ijk) u_i^i v_j^j w_k^k

ScalarTripleProduct is defined in the package  Calculus`VectorAnalysis` . We define here the operation MetricTripleProduct which groups all the operation performed above

(×) . //ToFlavor[red, black]//MetricTripleProduct[, g, e, h]

Print["or"] ; %//UpDownSwap[red @ k]

Warning : be sure that index 'h' does not appear in (u_i^i _i^i) × (v_j^j _j^j) . (w_k^k _k^k)

e_ (ijk)^(ijk) u_i^i v_j^j w_k^k

or

e_ (ijk)^(ijk) u_i^i v_j^j w_k^k

g^(1/2) is the volume of parallelepipedon which has the convariant (red) base vectors for its edges . Hence we have :

ℊ = Tensor[red @ g]//VolumeSquare[red @ g] ; Cross[d[red @ 1], d[red @ 2]]    - ℊ^(1/2) u[red @ 3]    /.TensorValueRules[]

{0, 0, 0}

Definition of an element of surface and of volume

d = dru[red @ i] d[red @ i]

d = dsu[red @ j] d[red @ j]

d = dtu[red @ k] d[red @ k]

dr_i^i _i^i

ds_j^j _j^j

dt_k^k _k^k

The volume element defined by the three vectors {dr, ds, dt}  is :

dV = (d×d . d//MetricTripleProduct[, g, e, h])/.h→k

Warning : be sure that index 'h' does not appear in (dr_i^i _i^i) × (ds_j^j _j^j) . (dt_k^k _k^k)

dr_i^i ds_j^j dt_k^k e_ (ijk)^(ijk)

Its explicit value is :

dV//LeviCivitaSimplify[e, ε][g, red]

dVval = %//VolumeSquare[red @ g]

(g)^1/2 dr_i^i ds_j^j dt_k^k ε_ (ijk)^(ijk)

3 dr_i^i ds_j^j dt_k^k ε_ (ijk)^(ijk)

In another reference frame this volume will remain unchanged. So we must be very careful that only the LeviCivita (e here) symbol is a tensor.
So, the correct transformation is :

"dV" == (dV//ToFlavor[black, red]) == dV

dV == dr_i^i ds_j^j dt_k^k e_ (ijk)^(ijk) == dr_i^i ds_j^j dt_k^k e_ (ijk)^(ijk)

Definition of an area element by the vector  dA  normal to it :

d = d×d//LinearBreakout[Cross][d[_], u[_]]//CrossProductExpansion[, e, k]

dd[l_] := d . d[l]//EvaluateDotProducts[, g]

(d§[red_ @ k_] = Tensor[d, {Void}, {red @ k}]) == dd[red @ k]

dr_i^i ds_j^j e_ (ijk)^(ijk) _k^k

d_k^k == dr_i^i ds_j^j e_ (ijk)^(ijk)

Note the possibility to use both FullForm (Tensor[...]) and Shortcut form to write an identity,
the two forms below being not litterally identical :

Tensor[d, {Void}, {red @ k}]

dd[red @ k]

d_k^k

dr_i^i ds_j^j e_ (ijk)^(ijk)

Pressure p of a fluid or a gas

Its product with an area dA,on which it acts,is a force dF normal to the area,i.e.it has the direction of dA,with components:

d = -p d ;

ResultFrame[res32 = dFd[red @ k] == -p dd[red @ k]]

      dF_k^k == -p dr_i^i ds_j^j e_ (ijk)^(ijk)       (3.2)

Weight of a volume element dV

The weight dW of a volume element dV is a vector (direction of the gravity field), the product of the volume and the specific weight ϒ :

ϒ = _h^h γ_h^h    and    dV = dr_i^i ds_j^j dt_k^k e_ (ijk)^(ijk)

hence

ResultFrame[res33 = d == ϒ dV]

      d == dr_i^i ds_j^j dt_k^k e_ (ijk)^(ijk) _h^h γ_h^h      (3.3)

dW also remains invariant by any change of frame. Explicitly we have,

(res33[[2]]//LeviCivitaSimplify[e, ε][g, red]//EinsteinSum[])/.PermutationSymbolRule[ε]//Simplify

ClearTensorShortcuts[{{, u, v, w, dr, ds, dt, dF, γ}, 1}, {{g, β, a, T}, 2}, {{ε, e, T}, 3}] ;

Created by Mathematica  (November 27, 2007) Valid XHTML 1.1!