4. Stress
Initialization
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We use conventionally an (over-) dot for the time derivative ( PartialD[_,t] ) :
![]()
![]()
The following values are taken as an example of a (red) basis frame :
![]()
![]()
![]()
![]()
![]()
![]()
and from equation (2.5) :
![]()
Figure 4.1 :
![[Graphics:HTMLFiles/index_21.gif]](HTMLFiles/index_21.gif)
Figure 4.1 Definition of stress.
To the triangle ABC, corresponds the area element dA:
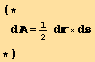
dA can also be expressed as functions of the vectors da, db, dc : dr = db – da and ds = dc – da,
![]()
![]()
![]()
If we choose the basis vectors along the three directions da, db, and dc
![]()
![]()
![]()
![]()
![]()
The covariant components ![]() of the vector dA element of surface
of the vector dA element of surface
![]()
![]()
![]()
![]()
![]()
For instance :
![]()
![]()
![]()
![]()
![]()
![]()
On the other hand, the triangle OAB can be represented by its outer normal,
![res = (1/2d×d//LinearBreakout[Cross][d[_]])//CrossProductExpansion[, e, k]//EinsteinSum[]//LeviCivitaOrder[e]](HTMLFiles/index_43.gif)
![]()
and we can verify that,
![]()
![]()
The four vectors, dA and ![]() db×da,
db×da, ![]() dc×da, and
dc×da, and ![]() dc×db add to zero.
dc×db add to zero.
Each force dP, dQ, dR and dF shown in the Figure, in an equilibrium stressed material, are proportional to the area on which it acts, and can be resolved into contravariant components,
![]()
![]()
![]()
![]()
![]()
![]()
![(*4.1*)d := σuu[red @ i, red @ j] dd[red @ i] d[red @ j] ResultFrame[res41 = "d" == d]](HTMLFiles/index_56.gif)
![]()

Figure 4.2 :
![[Graphics:HTMLFiles/index_59.gif]](HTMLFiles/index_59.gif)
Figure 4.2 Moment equilibrium of stresses.
Proof of the symmetry of the stress tensor ( ![]() ==
==![]() ) :
) :
The forces acting on the three faces are
![]()
![]()
![]()
![]()
![]()
On the opposite faces of the parallelepipedon, there are equal and opposite forces and, together, they form three couples, which have the moments
![]()
![]()

![]()
The sum of the three above moments must be zero at equilibrium.
![]()
![]()
so that each component of ![]() is zero.
is zero.
![]()
![]()
we take here the vector da, db, dc along the basis vectors as above.
![]()
![]()
and in the case k = 1.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Except the factor ![]() , the
, the ![]() are the contravariant components of dF acting on the parallelogram formed by
are the contravariant components of dF acting on the parallelogram formed by ![]() and
and ![]()
It is naturally possible to define the other components of the stresses. The stress components shown above are the most appealing.
Figure 4.4 :
![[Graphics:HTMLFiles/index_94.gif]](HTMLFiles/index_94.gif)
Figure 4.4 Stress components.
Relation between the stress and the strain. The Hooke's law gives the linear relation between their components.


![]()
The above relation is called the "Constitutive equation"
![]()
The tensor E, is symmetrical in {i,j} and in {l,m}, because on one hand ![]() is symmetrical in {l,m} :
is symmetrical in {l,m} :
![]()
![]()
![]()
![]()
while the symmetry of the stress tensor was proven in Section 4.
So there is only 36 different elements in E. But there is in addition a further reduction in number due to the existence of a strain energy :
The strain energy density S is given by :
![(*4.4*)ResultFrame[SequenceForm[" = ", res44 = = 1/2σuu[i, j] ℰdd[i, j]//ToFlavor[red, black]] ]](HTMLFiles/index_104.gif)
![]()
E (explicitely E§) and σ are symmetrical with respect to their indices.
So, S can be put into a standard order :
![]()
![]()
or in Cartesian coordinates, using conventional notations :

![]()
S =![]()
![]()
![]() is the total energy issued from the progressive application of a "force" from 0 to
is the total energy issued from the progressive application of a "force" from 0 to ![]() (which can be written t
(which can be written t ![]()
![]() , 0 ≤ t ≤1) during a "displacement"
, 0 ≤ t ≤1) during a "displacement" ![]() .
.
S is the sum ∫dS. So that if we write
![]()
we verify that S is recovered ( S§ ≡ S ):
![SequenceForm[ = § = , § = (∫_0^1 (d§)/tt)]](HTMLFiles/index_118.gif)
![]()
The factor 1/2 comes from the progressive application of the stress. For an infinitesimal increment of stress and strain, we will have,
![SequenceForm[d§ = , d$ = σuu[i, j] dℰdd[i, j]//ToFlavor[red, black]]](HTMLFiles/index_120.gif)
![]()
On the other hand, we can also differentiate S§. For this we need to simplify the derivation of a tensor component by another component of the same tensor (which must of course be independent). This is done using TensorComponentsD[g].
So that after differentiation :
![]()
![]()
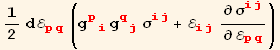
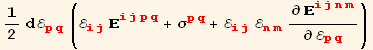
The third term in the parenthesis is zero, because E and E are independent. The increment of strain energy is then,
![]()
![]()
and,
![]()
![]()
![]()
This shows that we have also ![]() =
= ![]()
![]() , and that
, and that ![]() ≡
≡![]() . A symmetry between the pairs {i,j} and {p,q} has to be included.
. A symmetry between the pairs {i,j} and {p,q} has to be included.
This is summarized in the rule :
![]()
![]()
![]()
![]()
![]()
Here is the list of the 21 distinct elements of E (and similar lists in other basis) :
![]()
![]()
![]()
![]()
![]()
The Hooke's law
For an isotropic body we have the well known relations using the Young's modulus Ε, and the Poisson's ratio ν (we use here the notation σ$ for these particular values of the stress.
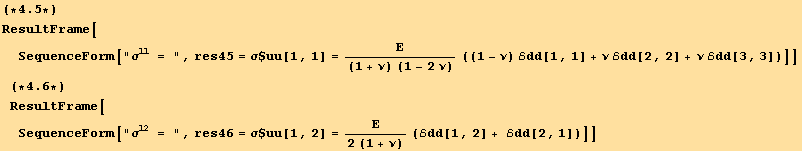
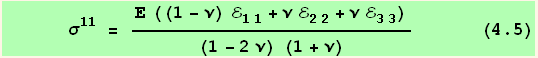
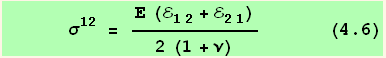
From which, using the constitutive equation ![]() =
= ![]()
![]() and the symmetry relations, we extract the
and the symmetry relations, we extract the ![]() . In the "black" cartesian basis :
. In the "black" cartesian basis :
![]()
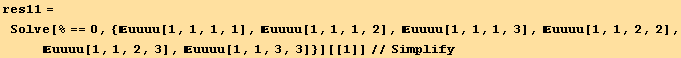
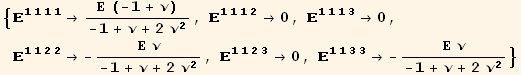
![]()
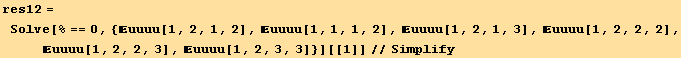
![]()
and all the cyclic permutations of {1,2,3}. In fact there is only 4 distinct and non-zero values :
![]()
![]()
![]()
![]()
![]()
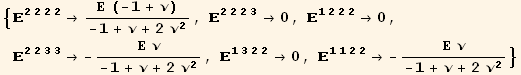
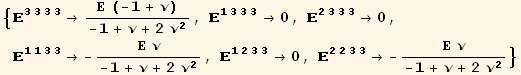
![]()
![]()
![]()
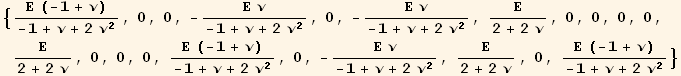
We can also introduce the Lame's coefficients λ and μ :
![(*4.7*)ResultFrame[LameRule = Solve[res47 = {-(Ε ν)/((ν + 1) (2 ν - 1)) == λ, Ε/(2 (ν + 1)) == μ}, {Ε , ν}][[1]]//Simplify]](HTMLFiles/index_170.gif)
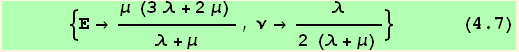
![(* In two dimensions we have (see below) *) (*4.8*)ResultFrame[res48 = {Ε->2μ (2μ + 2λ)/(2μ + λ), ν->λ/(λ + 2μ)}]](HTMLFiles/index_172.gif)
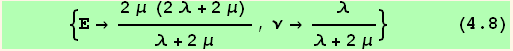
TABLE OF ELASTIC MODULI :
![]()
In the "black" canonical Euclidean basis the above relation can be summarized in the form :
![]()
![]()
![]()
Due to the tensorial character of the elastic moduli, we have in an arbitrary (red for instance) basis
![]()
![(*4.9*)ResultFrame[SequenceForm[uuuu[i, j, l, m], " = ", res49 = §uuuu[i, j, l, m]]//ToFlavor[red, black] ]](HTMLFiles/index_200.gif)
![]()
or using the Young's modulus Ε, and the Poisson's ratio ν (see LameRule above)
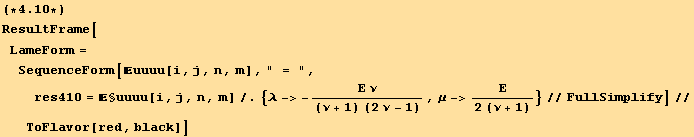
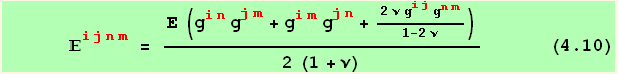
We recover the well known Lame rules defined above,
![]()
![]()
![]()
![]()
Example of an idealized porous material ( Flügge page 53 ).
It consists of thin walls of thickness t << a, parallel to the coordinate planes x, y, z. There are n walls in each directions.
Figure 4.5 :
![[Graphics:HTMLFiles/index_208.gif]](HTMLFiles/index_208.gif)
Figure 4.5 Model of a porous material.
From Hooke's law in two dimensions, obtained from the above relations,
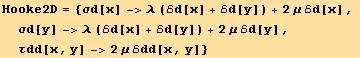
![]()
Relation between Lame coefficients and Poisson-Young modulus :
From above we define,
![]()
and we have the Poisson-Young relation in d=2 :
![]()
![]()
![]()
![]()
The first strain we impose to the porous material, is a simple stretching ![]() =
= ![]() in the x direction, with
in the x direction, with ![]() =
= ![]() = 0 and no shear strain. On the faces x = const this requires stresses in the vertical and in the horizontal walls. They add up to the force
= 0 and no shear strain. On the faces x = const this requires stresses in the vertical and in the horizontal walls. They add up to the force
![]()
![]()
The vertical walls normal to the x axis have no strain and no stress, and on the faces y = const (and idem z = const), we have only a contribution from the horizontal walls
![]()
![]()
![]()
![]()
The gross stress for the porous material is obtained by dividing each force by the gross area ![]() . Using for them the notation
. Using for them the notation ![]() ,
, ![]() ,
, ![]() , we have :
, we have :
![Stress2D = {σuu[1, 1] ->Fdd[x, x]/(n a)^2/.ruleFxx//Factor, σuu[2, 2] ->Fdd[y, y]/(n a)^2/.ruleFyy//Factor, σuu[3, 3] ->Fdd[z, z]/(n a)^2/.ruleFzz//Factor}](HTMLFiles/index_230.gif)
![]()
When the porous medium is submitted to a strain ![]() =
= ![]() or
or ![]() =
= ![]() , similar formulas hold, and for a combined stretching in all three directions we find
, similar formulas hold, and for a combined stretching in all three directions we find
![]()
and two similar equations. Now let us submit the medium to a shear strain ![]() =
= ![]() in the x,y plane. Then only the horizontal walls are stressed,
in the x,y plane. Then only the horizontal walls are stressed,
![]()
![]()
On the faces x = const and y = const the stresses add up to forces
![]()
![]()
from which we derive the gross stress
![]()
![]()
![]()
This gives the elastic constants:
![]()
![]()
![]()
![]()
![]()
![]()
The elastic coefficients are here very different from those of the isotropic solid.
In spite of the fact that the material shows the same elastic behavior in the three axis directions, it is not isotopic. This could be verified by a change in the axis. Flügge describes the example where the new orthonormal frame, let's call it green frame, has the axis ![]() in the direction {1,1,1} in the black frame, and
in the direction {1,1,1} in the black frame, and ![]() obtained by a rotation of 45° of the initial axis
obtained by a rotation of 45° of the initial axis ![]() . I will not detailed this example here.
. I will not detailed this example here.
Simpler form for the elastic law of isotropic bodies
We start from the constitutive equations,
![]()
![]()
![]()
![]()
![]()
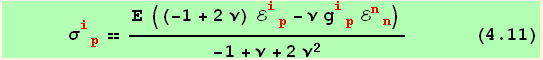
which gives using Lame coefficients :
![(*4.12*)ResultFrame[res412 = σud[red @ i, red @ p] == σ§§ud[red @ i, red @ p]/.LameRule//Simplify]](HTMLFiles/index_261.gif)
![]()
Inversion of the above relations
We first calculate ![]()
![]()
![]()
![]()
![]()
then determine ![]() :
:

![]()

![(*4.14*)ResultFrame[res414 = σud[red @ i, red @ i]/3 == ((HookesLaw2/.p→i//KroneckerContract[g])/.n→i//Simplify)/3 == K ℰud[red @ i, red @ i] ]](HTMLFiles/index_272.gif)
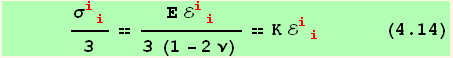
K is the bulk modulus of the material.
Hydrostatic stress s and cubic dilation e of are defined by the rule :
![]()
![]()
![]()
![]()
![]()
Strain and stress deviations
We introduce the strain deviation and the stress deviation by,

![]()
The following relation is verified :
![(*4.16*)ResultFrame[res416 = esrel = (Ε eud[red @ i, red @ j] == (1 + ν) sud[red @ i, red @ j])]](HTMLFiles/index_281.gif)
![]()
![]()
![]()
which is the relation obtained above (![]() ≡
≡ ![]() ). We can also write with the Lame moduli,
). We can also write with the Lame moduli,

![]()
Viscous fluids
In the case of isotropic viscous fluids, the stresses depend on the time derivatives of the strains (the strain rates). So we may use the above equations, simply replacing the strains by the strain rates :
![(*4.18*)ResultFrame[res418 = res417/.e->Overscript[e, .] ]](HTMLFiles/index_289.gif)
![]()
In the uni-axial tension test, a material is called ideally plastic if stress and strain are related according to the following rules :
i) they obey the Hooke's law σ = E ε for stresses σ < ![]()
ii) At the yield stress ![]() the strain can increase indefinitely without any restriction on the strain rate dε / dt except dε / dt > 0.
the strain can increase indefinitely without any restriction on the strain rate dε / dt except dε / dt > 0.
iii) the stress cannot be increased beyond ![]() .
.
Figure 4.8 :
![[Graphics:HTMLFiles/index_294.gif]](HTMLFiles/index_294.gif)
Figure 4.8 Stress-strain curve in ideal plasticity.
The yield limit is obtained when a certain function of all the stress components reaches a fixed value, and there exists as many yield conditions as there are materials. Some models are more commonly used, those of Tresca and of Mises. The latter is more easily convenient for a tensorial presentation. If the yield conditions cannot be derived from basic considerations, simple elementary concepts allow to derive plausible relations.
We can start from the strain energy density S, equ. (4.4), S = ![]()
![]()
![]() and introduce the stress and strain deviations equ. (4.15), and using the fact that the deviations
and introduce the stress and strain deviations equ. (4.15), and using the fact that the deviations ![]() and
and ![]() have a zero trace.
have a zero trace.

![]()
Using Hooke's law via equ (4.17), we have also,

![]()
Note : we have used two different notations (Tensor[e] and Tensor[Tensor[e]]) for the tensor e, so as to write the product e e, and not ![]() . This presentation could certainly be improved.
. This presentation could certainly be improved.
The first term in equ.(4.20) is a dilation energy, while the second is a distortion energy. As in plastic flow, there is practically no volume change, the plastic yield will depend entirely on the distortional part of the stress.
The Mises yield condition considers that the yield limit is reached when the distortion energy (![]() is symmetrical),
is symmetrical),
![]()
![]()
has reached a certain value characteristic of the material. Let say ![]()
![]() ==2
==2 ![]() ,
,
![]()
![]()
In terms of the actual stress ![]() (using (4.15))
(using (4.15))
![]()
![]()
![]()

![]()
and as a function of ![]() . This gives the Mises yield conditions, with the material constant k as a parameter.
. This gives the Mises yield conditions, with the material constant k as a parameter.
![]()
![]()
![]()

![]()
Physical meaning of the Mises conditions :
![]()
![]()
Case of a simple tension, ![]() =
= ![]() :
:
![((res421//EinsteinSum[])/.σud[red @ 1, red @ 1] → σ_x/.σud[i_, j_] →0) == 0(*4.23*)](HTMLFiles/index_329.gif)
![]()
![]()
![]()
Case of a simple shear, ![]() =
= ![]() =
= ![]() :
:
![((res421//EinsteinSum[])/. {σud[red @ 1, red @ 2] → τ_xy, σud[red @ 2, red @ 1] → τ_xy}/.σud[i_, j_] →0) == 0(*4.24*)](HTMLFiles/index_336.gif)
![]()
![]()
![]()
This shows that k is the yield stress in a simple shear, and that the Mises condition fixes the ratio between the yield limits in shear and uni-axial tension to 1:![]() .
.
Above the yield limit, the plastic flow begins. The flow between t and t+dt is defined by the components ![]() =
=![]() dt, and we have an incremental energy given by (see above) dS$ =
dt, and we have an incremental energy given by (see above) dS$ = ![]()
![]() ,
,
![]()
![]()
![]()
If the stress tensor changes by d![]() , where the new stress
, where the new stress ![]() +d
+d![]() satisfy the yield conditions, then there is a corresponding change in the strain and in the strain energy:
satisfy the yield conditions, then there is a corresponding change in the strain and in the strain energy:
![]()
![]()
It is here postulated that the change in the strain energy do not depend on the change of stress :
![]()
![]()
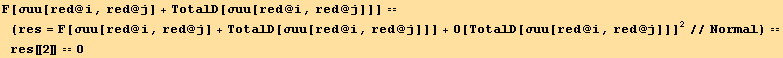
![]()
This last relation together with the preceding are fulfilled for all d![]() : hence their coefficients are proportional
: hence their coefficients are proportional
![]()
![]()
![]()
![]()
![]()
![Overscript[ℰ, .] _ (ij)^(ij) == μ ∂F/∂σ_ (ij)^(ij) (4.25)](HTMLFiles/index_363.gif)
![]()
![]()
![]()
![]()
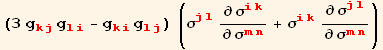
![]()
![]()
Using relation (4.15)
![]()

![]()
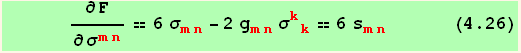
and together with (4.25) we obtain the strain rate :
![]()
![]()
![]()
![]()
This relation is known as the Mises-Reuss flow law.
![]()
| Created by Mathematica (November 27, 2007) |