5. Derivatives and Integrals
Initialization
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The following values are taken as an example of a (red) basis frame :
![]()
![]()
![]()
![]()
![]()
![]()
and from equation (2.5) :
![]()
![]()
When we want to differentiate a vector, we must differentiate the sum of the products of the components with the base vectors :
![]()
![]()
![]()
![]()
Introduction of the Christoffel symbols
ChristoffeluSymbol[e,Γ,k] is equivalent to the Christoffel notation used in Tensorial 4.0, which is the unique notation used there. We have also introduced here the covariant ChristoffeldSymbol[e,Γ,k]
The Christoffel symbols appear in the basis expansions of the partial derivatives of the basis vectors:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The Christoffel symbol are symmetrical with respect to the last two indices (see the proof below).
They can be put into a standard order using SymmetrizeSlots[] together with the constraint TensorSymmetry[Γ,3]=Symmetric[2,3] (which is now in Tensorial4, and replaces most of the time (but not always) SymmetricStandardOrder[Γ,{2}])
![]()
![]()
![]()
![]()
![]()
![]()
I will be necessary in the following to make the equivalence between partial derivatives with respect to the basis coordinates xu[i] and the partial derivatives with respect to the indices, using PartialToDif :
Examples :
1)
![]()
![]()
![]()
The labels and the coordinates must of course agree. If they do not, the indices are not used :
![]()
![]()
2) The reverse writing needs to introduce the labels :
![]()
![]()
![]()
![]()
Derivation of a vector v
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Print[but the following results cannot exist !!]](HTMLFiles/index_58.gif)
![]()
![]()
![Print[as only the first index in Γ is tensorial and can be raised and lowered]](HTMLFiles/index_61.gif)
![]()
![]()
![]()
![]()
![]()
The symmetry of the two last indices of the Christoffel symbols comes from the commutation of the second derivatives, and we have,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Explicit expression of the Christoffel symbols
Note : PartialD involving only indices does not use all the properties of partial derivatives. To include them we need to go through explicit partial derivations via the labels {x,δ,g,Γ}. This is obtained using DifToPartialD[labels]. PartialDToDif restores the index notation.
![PartialD[d[red @ j] . d[red @ k], red @ i] + PartialD[d[red @ k] . d[red @ i], red @ j] - PartialD[d[red @ i] . d[red @ j], red @ k]](HTMLFiles/index_75.gif)
![]()
![]()
![]()
![]()
![]()
so that we have the explicit expression for the Christoffel symbols :

![]()
We see that with the notation "upper index in the third position", the above proof is immediate.
Covariant Derivative
Important remarks :
CovariantD is applied only over objects in the simple tensor shape without partial derivatives involved.
Mathematically the covariant derivative is only defined over strict tensors and a partial derivative is not a strict tensor.
Mathematically we are allowed to take covariant derivatives of other objects such as the first order total derivative or the non-expanded TotalDerivative or LieDerivative but they are not implemented because it could be too complicated for the general case. (It is preferable to have Tensorial sharp limitations rather than fuzzy ones)
What we can do instead is to take the Covariant derivative of a simple tensor object, expand it and replace the values in the expanded expression. The calculation of the acceleration components is an example of this where we do not take the Absolute derivative of the Total derivative of the position directly.
The partial derivative can be taken over anything as well as the Total derivative but the Absolute derivative is like the Covariant derivative.
![]()
![]()
![]()
![]()
so that the quantity,
![]()
![]()
is the i-component of the j-derivative of v. It is the covariant derivative of v.
![]()
![]()
This result is of course directly given by the operation ExpandCovariantD :
![]()
![]()
similarly, the covariant derivative of the covariant component ![]() is given by,
is given by,
![]()
![]()
![]()
![]()
or also,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
As φ is a scalar, Dφ is also a covariant derivative Dcovφ :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The term ![]() -
-![]()
![]() -
-![]()
![]() gives the covariant derivative
gives the covariant derivative ![]() of
of ![]() .
.
Of course, we can verify that this directly obtained using ExpandCovariantD :
![]()
![]()
and the three other equivalent expressions,
![]()
![]()
![]()
![]()
![]()
![]()
Application : Derivative of a force
![]()
![]()
![]()
![]()
The covariant derivative (in the above expression ![]() ) of the basis vectors are zero.
) of the basis vectors are zero.
![]()
![]()
![]()
![]()
Also the covariant derivative of the tensor g is zero :
![]()
![]()
which derivative is explicitely :
![]()
![]()
![]()
![]()
See Fluegge p.72 for an intuitive explanation of ![]() ≡ 0.
≡ 0.
All this is summarized in the operator CovariantDSimplify[e,g,e] . Coming back to the covariant derivative of dF we have :
![]()
![]()
Now let us choose at ![]() and
and ![]() + d
+ d![]() two area elements dA equal in size and orientation. Then
two area elements dA equal in size and orientation. Then ![]() = 0 and hence
= 0 and hence ![]() = 0 and the derivative of the force dF is,
= 0 and the derivative of the force dF is,
![]()
This vanishes, for any choice of the components ![]() of the two section elemnts, if and only if
of the two section elemnts, if and only if ![]() = 0. Each of the 27 quantities
= 0. Each of the 27 quantities ![]() expresses one aspect of the rate of change of the stress tensor, namely the j-component of the change of the force as far as it depends on the i-component of dA. Vanishing of all the components of the covariant derivative means that between adjacent points the physical stress does not change.
expresses one aspect of the rate of change of the stress tensor, namely the j-component of the change of the force as far as it depends on the i-component of dA. Vanishing of all the components of the covariant derivative means that between adjacent points the physical stress does not change.
Case for the Levi-Civita tensors
As the covariant derivatives of the metric tensor are zero, it is also the case for the Levi-Civita tensor which only depends on the determinant of the metric tensor. As a consequence :
![]()
![]()
![]()
![]()
(*5.4*)
ResultFrame[
res54=(res[[1]]//PartialDToDif)==res[[2]]==(eddd[1,2,3]Γudd[m,k,m]//ToFlavor[red,black])
]
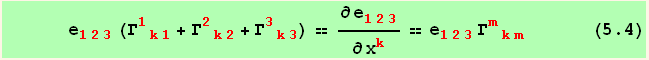
The Riemann-Christoffel tensor ![]()
By definition :
![(*5.5*)ResultFrame[res55 = (res = (CovariantD[vd[red @ i], {red @ j, red @ k}] - CovariantD[vd[red @ i], {red @ k, red @ j}])) == vd[red @ m] (Ruddd[m, i, j, k]//ToFlavor[red, black])]](HTMLFiles/index_162.gif)
![]()
Explicit expression of the Riemann-Christoffel tensor :
![]()
![]()
![]()
![]()
![]()
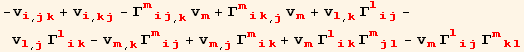
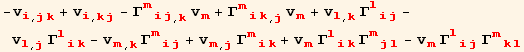
![(*5.6*)ResultFrame[res56 = (Ruddd[m, i, j, k]//ToFlavor[red, black]) == Coefficient[res, {vd[red @ m]}] ]](HTMLFiles/index_171.gif)
![]()
![]()
BasisDerivation assign to zero covariant derivatives of basis vectors, and express their partial derivatives using Christoffel symbols.
It is used here to prove the relation ![]() ==
==![]() (
(![]() +
+![]()
![]() ).
).
Examples
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
DivToCov will be used to write a partial derivative as a function of its covariant derivative corrected by the Christoffel contribution :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The first partial derivative of a vector is identical to its covariant derivative :
![]()
![]()
![]()
![]()
![%[[1]] + (%[[2]]/.{i→k, m→i}) ; =. ; <br />(*5.7*)](HTMLFiles/index_199.gif)
![]()
![]()
The second partial derivative of a vector contains a correction to its second covariant derivative, involving a Christoffel symbol :
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![res58 = T == d[red @ i] (resa[[Range[4]]] + (resa[[5]]/.{m→h}) + (resa[[6]]/.{m→h, h→m})//SymmetrizeSlots[]) ; (*5.8*)](HTMLFiles/index_210.gif)
![]()
![]()
Gradient, Divergence and Curl
Relation between the standard definitions included in Mathematica and the present tensorial definition.
![]()
Gradient
![]()
![]()
In tensorial notations, the gradient (we use the notation TGrad) is defined as,
![]()
![]()
![]()
Divergence
![]()
![]()
In tensorial notations, the divergence (we use the notation TDiv) applied to u or v gives,
![]()
![]()
![]()
![]()
![]()
![]()
Curl :
![]()
In tensorial notations, the curl (we use the notation TCurl) is defined as,
![]()
![]()
Curl of a vector expressed in the red basis and calculated in the blue one :
![]()
![]()
![]()
![]()
Option False allows to leave the basis changes β unexpressed. Note that the basis changes can have non-zero convariant derivatives
![]()
![]()
![]()
![]()
Laplacian
![]()
![]()
![]()
![]()
We can also check that a gradient field has no curl : the second covariant derivative of a scalar tensor is symmetrical with respect to i and j while the LeviCivita symbol is antisymmetrical.
![]()
![]()
![]()
![]()
![]()
![]()
and that a curl field has no divergence
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Integral theorems of Stokes and Gauss
Gauss theorem in two dimensions :
Consider an element ds of a close curve C on a surface S; C is the contour of a domain A :
![]()
Suppose that ![]() is the vector normal to S at the considered point of C. dn is the vector tangent to S and normal to C.
is the vector normal to S at the considered point of C. dn is the vector tangent to S and normal to C.
Integration of a vector field v in S. First integrate along the contour ABCD of the figure :
Figure 5.3
![[Graphics:HTMLFiles/index_258.gif]](HTMLFiles/index_258.gif)
Figure 5.3 Area element.
![d×d[red @ 3] ; d = %//LinearBreakout[Cross][d[_]]//CrossProductExpansion[, e, h] d§ = %/.ds->dr](HTMLFiles/index_259.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![BC = (( + CovariantD[, red @ k] dru[red @ k]//CovariantDSimplify[, g, e]//Factor) . d//EvaluateDotProducts[, g])//LeviCivitaOrder[e]](HTMLFiles/index_268.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![".d == " %/.((-eddd[i, j, 3] dru[i] dsu[j]//SumExpansion[i, j, k]//LeviCivitaOrder[e]) :> -dAd[red @ 3]//ToFlavor[red, black]//FullSimplify)](HTMLFiles/index_276.gif)
![]()
The second term in parenthesis is TDiv v in two dimensions. Now assembling together such quadrilaterals to fill the area A, gives the Gauss theorem in d = 2 :
![]()
Gauss theorem in three dimensions :
Figure 5.5
![[Graphics:HTMLFiles/index_279.gif]](HTMLFiles/index_279.gif)
Figure 5.5 Volume element.
![d := dru[red @ j] d[red @ j] d := dtu[red @ k] d[red @ k] {d, d, d}](HTMLFiles/index_280.gif)
![]()
![]()
We calculate for the volume element defined by {dr, ds, dt} the surface integral ∫vdA = ∫![]() d
d![]()
The surface delimited by the vector {ds, dt} is associated to the vector
![]()
![]()
![]()
so, for the two opposite faces defined by {ds, dt} (Note the subtility between Tensor... and its ShortCut )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The contribution of the other two pairs of faces of the volume element are obtained by cyclic permutation of the free indices {i j k} :
![]()
![]()
which can then be compared to result ( ![]()
![]()
![]()
![]()
![]() ) :
) :
![]()
![]()
so that the two last expressions are identical :
![]()
![]()
This constitute the three dimensional form of the divergence theorem of Gauss :
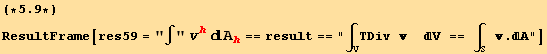
![]()
Stokes theorem in two dimensions :
Figure 5.6
![[Graphics:HTMLFiles/index_309.gif]](HTMLFiles/index_309.gif)
Figure 5.6 Triangular area element.
The triangle represented in the figure has an area represented by the vector,
![]()
![]()
We calculate now the integral along the counterclockwise contour ABCA. On each three sides (![]() ,
, ![]() -
- ![]() , -
, - ![]() ) we have an average value :.
) we have an average value :.
![]()
![]()
![]()
![]()
![]()
Including this last result into the integral along the perimeter of ABCA gives
![]()
![]()
which is equal to TCurl[u].dA
![]()
![]()
![]()
![]()
Covering any area A with contour C with triangles of this kind leads to the cancellation of all the terms from adjacent sides of the infinitesimal triangles so that only the integration along C remains.
Stokes' theorem is then :
![(*5.1*)ResultFrame[res510 = ∫ s == ∫ (TCurl ).A] \C \A](HTMLFiles/index_327.gif)
![]()
Vector field versus scalar and solenoidal fields
![]()
Given a vector field u, find the scalar field φ of which it is the gradient, or a vector field w of which it is the curl;
If TCurl u = 0 then u = TGrad φ
If TDiv u = 0 then u = TCurl w
so, every vector field may be split (in more than one way) into a gradient field and a solenoidal field, and
![ud[red @ i] == CovariantD[Tensor[φ], red @ i] + (CovariantD[wu[red @ k], red @ h] guu[red @ h, red @ j]) eddd[red @ i, red @ j, red @ k]//MetricSimplifyD[g] (*5.11*)](HTMLFiles/index_330.gif)
![]()
![]()
![]()
where φ is a scalar potential, and ![]() a vector potential
a vector potential
![]()
| Created by Mathematica (November 27, 2007) |