7. Special Problems of Elasticity
Initialization
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
and from equation (2.5) :
![]()
Plane Strain
In plane strain, the considered object is a cylindrical or prismatic body along z = ![]() , loaded in such a way that all stresses and deformations are independent of z.
, loaded in such a way that all stresses and deformations are independent of z.
The two other coordinates, ![]() , α = {1,2} are the coordinates possibly curvilinear in the plane {x, y} perpendicular to z.
, α = {1,2} are the coordinates possibly curvilinear in the plane {x, y} perpendicular to z.
We define a new system of base indices in the {x,y} plane :
![]()
![]()
![]()
![]()
![]()
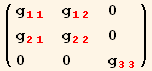
We will use greek indices to designate components in the {x,y} plane, and we can verify that the scalar products of basis vectors ![]() with
with ![]() gives zero.
gives zero.![]() is then a metric tensor for the 2d subspace {1,2}.
is then a metric tensor for the 2d subspace {1,2}.
![]()
![]()
![]()
![]()
![]()
As the partial derivative ![]() of
of ![]() in the {x,y} plane remains in this plane, its scalar product with
in the {x,y} plane remains in this plane, its scalar product with ![]() gives zero :
gives zero :
![]()
![]()
![]()
![]()
![]()
![]()
For similar reasons :
![]()
![]()
![]()
![]()
![]()
![]()
and this is verified for all Christoffel symbols in which one or more of its indices are equal to 3.
A vector v,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
As noticed above, the second term ![]()
![]() vanishes. First, let i = α, j = β; then
vanishes. First, let i = α, j = β; then
![]()
![]()
which is simply equation (5.2) in the two dimensional subspace. Now, let i = α, j = 3; then
![]()

![]()
![]()
![]()
![]()
When i = 3, j = β; then
![]()
![]()
and if i = 3, j = 3; then
![]()
![]()
and similarly :
![]()
![]()
![]()
![]()
In all these cases (and this can be generalized to covariant components) the covariant derivative is equal to the partial derivative.
Now, in plane strain, the third displacement component ![]() = 0 and the displacement u,
= 0 and the displacement u,
![]()
![]()
The kinematic equation (6.2)
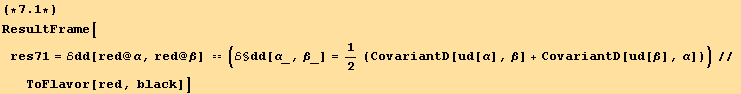
![]()
while the other formulas gives (and in the present case the covariant derivatives are equal to usual derivatives),
![]()
![]()
![]()
![]()
In the first ( α = 1,2 ) equations, ![]() does not depend on
does not depend on ![]() , and
, and ![]() = 0, and in the second equation again
= 0, and in the second equation again ![]() = 0, so that
= 0, so that
![]()
![]()
For a general anisotropic material, the constitutive equation (4.3) gives
![]()
![]()
and due to (7.1),
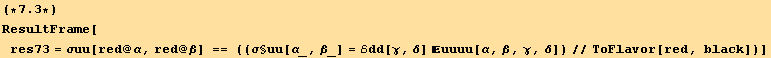
![]()
In addition, there is a stress,
![(*7.4*)ResultFrame[res74 = σuu[red @ 3, red @ 3] == (σ§uu[3, 3]//ToFlavor[red, black])]](HTMLFiles/index_95.gif)
![]()
necessary to keep ![]() ==0. But we can have in addition, if the corresponding moduli are nonzero,
==0. But we can have in addition, if the corresponding moduli are nonzero,
![(*7.5*)ResultFrame[res75 = σuu[red @ α, red @ 3] == (σ§uu[α, 3]//ToFlavor[red, black])]](HTMLFiles/index_98.gif)
![]()
This case will be considered later. For the moment, only plane anisotropy will be considered.
Equation (7.2) can be inverted, as there is three linear equations for αβ=={11,12,22}, and three unknowns {![]() ,
,![]() ,
,![]() }.
}.
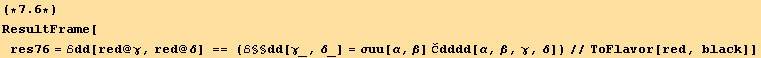
![]()
![]()

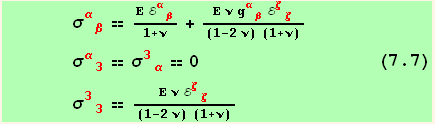
while the inverted formulas lead to,
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
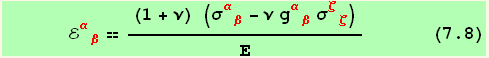
Equilibrium conditions
It is easily obtained from (6.5), using the fact that ![]() = 0,
= 0,
![(*7.9*)ResultFrame[res79 = Xu[red[α]] + CovariantD[σuu[red[β], red[α]], red[β]] == 0 ]](HTMLFiles/index_119.gif)
![]()
Equations (7.1), (7.9), or also (7.3), (7.6) or (7.7), are eight components equations for eight unknowns {![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() }.
}.
To eliminate a maximum of unknowns we can,
1) introduce (7.3) into (7.9)
If we want to leave the ![]() unexpanded we can use HoldOp or Tensor[
unexpanded we can use HoldOp or Tensor[![]() ] :
] :

![]()
and then use (7.1)
![]()
![]()
![]()
![]()
If the material is homogeneous, ![]() = 0,
= 0,
![(*7.1*)ResultFrame[res710 = res1/.CovariantD[uuuu[α_, β_, γ_, δ_], red[η_]] →0]](HTMLFiles/index_138.gif)
![]()
In the isotropic case (7.1) and (7.7) lead to,
![]()
![]()
![]()
![]()
![]()
![]()
![res/. u_ζ^ζ^(; ζα) → u_ζ^ζ_ (; ζ)^(; α)/.ζ→β//SymmetricStandardOrder[u, {2, 3}]//Simplify(*7.11*)](HTMLFiles/index_146.gif)
![]()
![]()
![]()
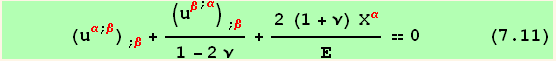
which is a particular case of (7.10).
Equations (7.10) and (7.11) are a pair of simultaneous differential equations of second order. Boundary conditions to be imposed to displacements or stresses can be easily formulated in terms of ![]() and
and ![]() .
.
Second method
We postulate that the stress components are the second derivatives of a scalar field Φ. ![]() are the Levi-Civita tensors in two dimensions.
are the Levi-Civita tensors in two dimensions.
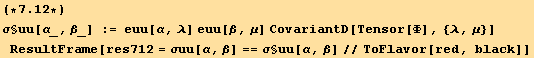
![]()
![]()
![]()
This leads to two equations, with α = 1,2. When α is fixed, λ is also fixed (α = 1,2 → λ = 2,1). The factor associated with ![]() , is
, is ![]()
![]() , which is zero because
, which is zero because ![]() is antisymmetrical while
is antisymmetrical while ![]() is symmetrical in {β,μ}. So that,
is symmetrical in {β,μ}. So that,
![]()
![]()
which is equation (7.9) in absence of force. We can generalize this in the case the force ![]() is conservative. The
is conservative. The ![]() derives from a potential :
derives from a potential :
![]()
![]()
If we replace (7.12) by

![]()
we have,
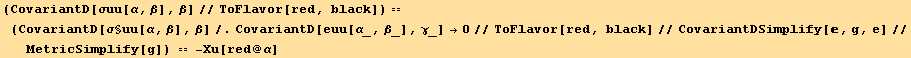
![]()
which corresponds to equation (7.9). We will use now equation (7.14). We need there an equation for Φ ; for that we use the kinematic equation (7.1), and the Hooke's law (7.6).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
the right-hand-side of the last equation gives zero for symmetry reasons, so that :
![]()
![]()
This equation is nothing but the compatibility equations in two dimensions, which could have also been derived from (6.4) by restricting the dummy indices to the two-dimensional range.
Now, using Hooke's law (7.6),
![]()
![]()
Then we express ![]() in terms of Φ (equ. )
in terms of Φ (equ. )
![]()
![]()
The covariant derivatives of the Levi-Civita tensor are zero,
![]()
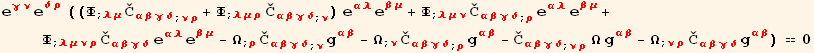
in addition, if the material is homogeneous (though still anisotropic), the covariant derivatives of the compliance ![]() are also zero :
are also zero :

![]()
![]()
In the isotropic case we can replace (7.6) by (7.8),
![]()
![]()
![]()
![]()
![]()
![]()
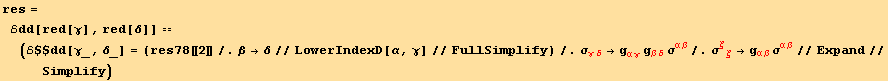
![]()
which, introduced in the compatibility conditions (7.14),
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This last equation is again of the fourth order. But it can be drastically simplified:
The left hand side gives,
![]()
![]()
![]()
![]()
![]()
and the right hand side,
![]()
![]()
Or finally an equation of the very simple form,
![]()
![]()
and even, in the absence of body force,
![]()
![]()
This is a bilaplacian form in two dimensions.
![]()
![]()
Plane Stress
Having studied plane strain, we now turm to plane stress. We restrict ourselves to slabs of constant thickness h. On the faces ![]() =±h/2 there are no external forces so that the stresses
=±h/2 there are no external forces so that the stresses ![]() =
= ![]() = 0. Because the slab is thin, we can suppose that these stress components remain zero across its thickness, while the strain can vary.
= 0. Because the slab is thin, we can suppose that these stress components remain zero across its thickness, while the strain can vary.
We start from the elastic law (4.3) in the anisotropic case, inverted,
![]()
![]()
For the plane stress system, it yields the strains,

![]()
![]()
![]()
We will assume, as it is generally the case that ![]() = 0. When (7.18) is inverted, this gives,
= 0. When (7.18) is inverted, this gives,
![]()
![]()
where the ![]() are different from the
are different from the ![]() of the 3d law.
of the 3d law.
If we consider an isotropic case, we start from (4.13), and let ![]() =
= ![]() =
= ![]() = 0, together with the structure of g,
= 0, together with the structure of g,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
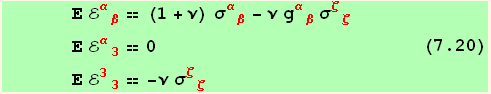
This equation (7.20) can be easily inverted :
![]()
![]()


![]()
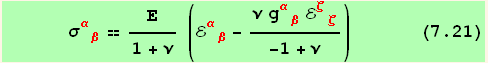
Having the elastic law, we can deduce a differential equation similar to (7.10), except that now E is replaced by Ê
![]()
![]()
![]() being a metric tensor in the 2d subspace, we can raise and lower the indices, and write,
being a metric tensor in the 2d subspace, we can raise and lower the indices, and write,
![]()
![]()
![]()
![]()
In the isotropic case, (7.11) is then replaced by (using 7.21),
![]()
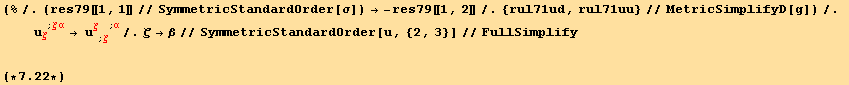
![]()
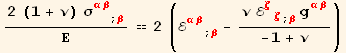
![]()
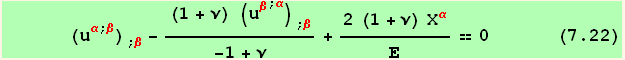
which slightly differs from (7.11), by the factor of ![]() .
.
If we consider the second way described above (using Φ ), the definition (7.12) and its alternative (7.13) remain unchanged, as well as the compatibility conditions (7.14). For anisotropic materials, (7.18) replaces (7.6), and in (7.15) the compliances Č replace the 3d compliances C. In the isotropic case, (7.20) (Ε ![]() ==(1+ν)
==(1+ν) ![]() -ν
-ν ![]()
![]() ) replaces (7.8) (Ε
) replaces (7.8) (Ε ![]() ==-(1+ν) (-
==-(1+ν) (-![]() +ν
+ν ![]()
![]() )). Replacing (7.16), (7.20) leads to
)). Replacing (7.16), (7.20) leads to

![]()
or,
![]()
![]()
Generalized Plane Strain
Figure 7.2
![[Graphics:HTMLFiles/index_291.gif]](HTMLFiles/index_291.gif)
Figure 7.2 Element of an anisotropic material.
In figure 7.2, the shading indicates the direction of some fibers or grain, i.e. the principal direction of elasticity. When a tensile stress ![]() is applied, the right angles of the element will not be conserved, unless a shear stress
is applied, the right angles of the element will not be conserved, unless a shear stress ![]() of a certain magnitude is also applied. Both stresses must occur if the deformation is nothing but a strain
of a certain magnitude is also applied. Both stresses must occur if the deformation is nothing but a strain ![]() . The shear stresses are subject to an equilibrium condition given by (6.5) with i=3 and
. The shear stresses are subject to an equilibrium condition given by (6.5) with i=3 and ![]() = 0.
= 0.
![]()
![]()
The presence of the new stresses leads to new strains via the Hooke's law. We have to admit the existence of a third displacement ![]() =w, function of
=w, function of ![]() , but not of
, but not of ![]() . The Hooke's law gives in its inverted form,
. The Hooke's law gives in its inverted form,
![]()
![]()
![]()
or, separating the third component and using the symmetries,

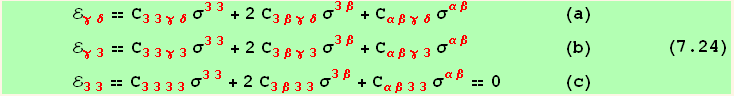
Considering now the kinematic relations (7.1),
![]()
![]()
and the additional relation (now with a covariant derivative here),
![]()
![]()
Since ![]() does not depend upon
does not depend upon ![]() , and since
, and since ![]() = w, we have
= w, we have
![]()
![]()
The new compatibility conditions are obtained by differentiation :
![]()
![]()
which can be written with the antisymmetric Levi-Civita tensor,

![]()
![]()
![]()
In addition, the equilibrium conditions (7.9) must be introduced. In absence of external force
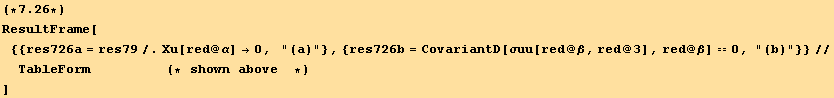
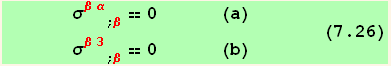
The number of independent equations issued from (7.24), the compatibility conditions (7.14) and (7.25), and the equilibrium (7.26), is 6+2+3=11, equal to the number of unknows (6 stresses and 5 strains) excluding ![]() which is zero.
which is zero.
We can also satisfy the equilibrium condition (7.26), introducing the stress function Φ as in (7.12), and a second function Ψ to take into account (7.26b) such that,
![(*7.27*)ResultFrame[res727 = σuu[red @ 3, red @ α] == euu[red @ α, red @ λ] CovariantD[Tensor[Ψ], red @ λ]]](HTMLFiles/index_324.gif)
![]()
Remains now the two stress function and the stress ![]() for which we need to establish three equations. Two of them are based on the compatibility conditions (7.14) and (7.25). The third equation comes from (7.24c) together with (7.27), Together with the elastic law to introduce the stresses, and with (7.27) and (7.12) this gives for any anisotropic but homogeneous material.
for which we need to establish three equations. Two of them are based on the compatibility conditions (7.14) and (7.25). The third equation comes from (7.24c) together with (7.27), Together with the elastic law to introduce the stresses, and with (7.27) and (7.12) this gives for any anisotropic but homogeneous material.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![res728c = (%[[2]]//Simplify) == 0 ; <br />(*7.28*)](HTMLFiles/index_342.gif)
![]()
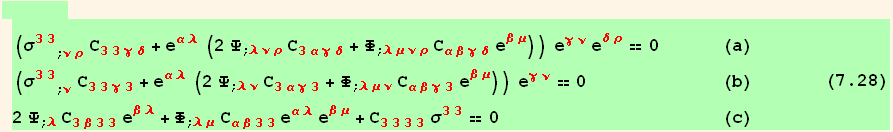
Moreover it is easy to eliminate ![]() in these equations :
in these equations :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![res729b = ((%[[1, 1]]/.β→α//Factor) + %[[1, 2]]) %[[2]] == 0 ; <br />(*7.29*)](HTMLFiles/index_353.gif)
![]()
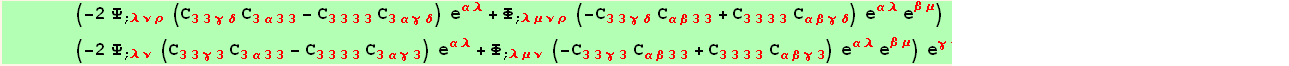
To summarize, we have here a system of two differential equations in Φ and Ψ. It is of order six, while we had only one equation of order one in the isotropic or plane anisotropy cases.
If we limit the above equations to the case of plane anisotropy, we shall have (![]() ≠ 0). To these two equations we must associate equation (7.24c) for
≠ 0). To these two equations we must associate equation (7.24c) for ![]() :
:

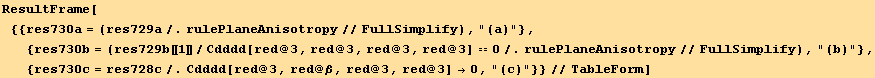
![]()

We can easily verify that (7.30a) is identical to equation (7.15) for Ω ≡ 0.
![]()
![]()
![]()
![]()
![]()
![]()
to prove this we use the elastic law which are here,
![]()
![]()
![]()
![]()
and eliminate ![]() and compare to (7.6),
and compare to (7.6),
![]()
![]()
![]()
![]()
gives for a coefficient ![]() in (7.30a) (
in (7.30a) (![]() factors out and drops) :
factors out and drops) :
![]()
![]()
Remains equation (7.30b) : ![]()
![]()
![]()
![]() ==0. The stress function Ψ is related to the shear stresses
==0. The stress function Ψ is related to the shear stresses ![]() (see (7.27), normal to the planes
(see (7.27), normal to the planes ![]() = const. The shear compliances
= const. The shear compliances ![]() connect these stresses to the strains
connect these stresses to the strains ![]() (see (7.24b)) :
(see (7.24b)) :
![]()
![]()
Torsion
![[Graphics:HTMLFiles/index_391.gif]](HTMLFiles/index_391.gif)
Figure 7.3 Torsion bar.
We consider here a straight bar of constant cross section. The coordinates ![]() are in the cross section and z =
are in the cross section and z = ![]() is is in the direction of the generators of the cylindrical surface. It is associated with a monoclinic coordinate system and
is is in the direction of the generators of the cylindrical surface. It is associated with a monoclinic coordinate system and ![]() = 0,
= 0, ![]() = 1.
= 1.
A couple M (Figure 7.3) is applied to the ends of the bar. In each cross sections, there is a shear stress ![]() ==
==![]()
![]()
![]()
The deformation, essentially a rotation Ψ of the cross sections linear with z, with a twist θ,
![]()
![]()
To first order the cross section does not change its shape, so that,
![]()
![]()
and so,
![]()
![]()
and hence,
![]()
![]()
![]()
The interchangeability of the covariant derivatives leads to,
![]()
which has no solution except,
![]()
![]()
The rotation, defined by equation (6.3),
![]()
![]()
![]()
gives,

![]()
A displacement ![]() ==wof the cross section, normal to the plane of the cross section, takes place. It depends on
==wof the cross section, normal to the plane of the cross section, takes place. It depends on ![]() , but not on z.
, but not on z.

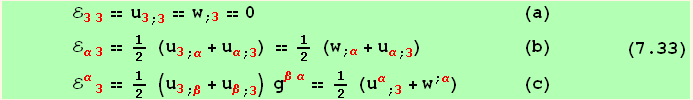
Due to the symmetry of the order of derivation, we have the relation,
![]()
![]()
so that using (7.31) and (7.32b),

![]()
and also,
![]()
![]()
If we introduce the strains (7.31) and (7.33a) in Hooke's law (4.11),
![]()
![]()
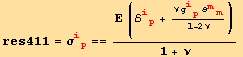
![]()
![]()
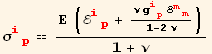
we see that,

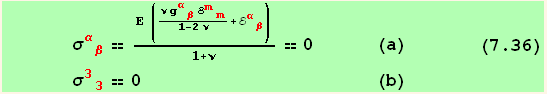
The only non vanishing stress components are
![(res411/.{i→α, p→3}/.Tensor[g, {red[α], Void}, {Void, red[3]}] →0) ; (*7.37*)](HTMLFiles/index_436.gif)
![]()
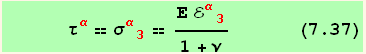
This equation, with (7.35) leads to,

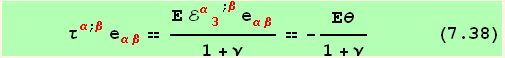
and with the equilibrium condition (6.5) in absence of body force, and for i = 3 and j = α,
![res65 = Tensor[X, {red[i]}, {Void}] + CovariantD[Tensor[σ, {red[j], red[i]}, {Void, Void}], red[j]] == 0 ; (*7.39*)](HTMLFiles/index_441.gif)
![]()
![]()
A way to satisfy identically equation (7.39), is to write the stress components as derivatives of a stress function Φ :
![]()
![]()
Using (7.38) leads to a differential equation for Φ :
![]()
![]()
This last expression can be simplified using FullLeviCivitaExpand
![]()
![]()
![]()
![]()
Equation (7.41) is the differential equation for the torsion problem.
Boundary conditions to be imposed upon Φ :
The only load applied to the torsion bar is a torque M on both ends. The cylindrical surface is free of external tractions. In particular ![]() = 0 and the shear stress vector
= 0 and the shear stress vector ![]() at the boundary point of the cross sections must have no component normal to the boundary.
at the boundary point of the cross sections must have no component normal to the boundary.
The stress vector ![]()
![]() is hence parallel to line vector elements
is hence parallel to line vector elements ![]()
![]() . This can be imposed by the vanishing cross product
. This can be imposed by the vanishing cross product
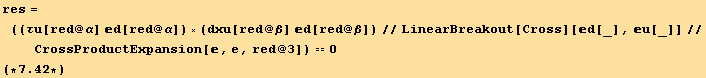

![]()
![]()
Making use of (7.40) ,
![]()
![]()
![]()
![]()
The last equation means that Φ is constant along the boundary.
![]()
![]()
If the cross section is simply connected we can set ![]() ==0, because
==0, because ![]() is defined up to a constant. If the cross section has one or several holes, we can choose
is defined up to a constant. If the cross section has one or several holes, we can choose ![]() ==0 on one of the separate curve, in general the external boundary. The values of
==0 on one of the separate curve, in general the external boundary. The values of ![]() along the edges of the holes follow the requirement that the warping displacement w is a unique function of
along the edges of the holes follow the requirement that the warping displacement w is a unique function of ![]() .
.
To formulate this we write :
![]()
![]()
![]()
![]()
We solve this equation where w is a scalar tensor
![]()
![]()
and integrate along a closed curve lying entirely inside the material (where w ≠ 0 ). Uniquiness of w requires that this contour integral vanishes :
NB : we use here, in this version, the contour integration ∮ only as a notation (but see Paul Abbott, "Contour Integration", for practical use of ∮ in calculations).

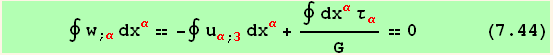
!["∮"CovariantD[Tensor[w], red @ α] dxu[red @ α] == ∫_x0^x1w^′[x_α^α] xu[red @ α] %/.x1→x0](HTMLFiles/index_481.gif)
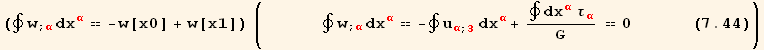
Now we use Stokes' theorem \!\(∫\_\(\(\\ \)\(C\)\)\)u ds ==\!\(∫\_\(\(\\ \)\(A\)\)\)(TCurl u).dA to calculate,
![]()
![]()
![]()
![]()

![]()
![]()
with the area element,
![]()
![]()
If we express ![]() in terms of θ (via 7.34) :
in terms of θ (via 7.34) :
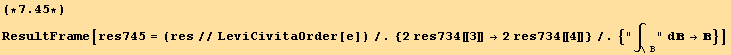
![]()
and from (7.44) and (7.40), we obtain the relation satisfied by the stress function, when the integral is extended over anyone of the interior boundaries of the cross section.
![]()
![]()
![]()
If the cross section possess n holes, the procedure is as follows :
- Find the solution ![]() of (7.41) which satisfy
of (7.41) which satisfy ![]() ==0 on all boundaries.
==0 on all boundaries.
- Calculate the solutions ![]() , k = 1 ,2,..., n, of the homogeneous equation
, k = 1 ,2,..., n, of the homogeneous equation ![]() = 0 which satisfy
= 0 which satisfy ![]() ==1 on the boundary of the kth hole and
==1 on the boundary of the kth hole and ![]() ==0 on all other boundaries.
==0 on all other boundaries.
- Evaluate (7.46) for each interior boundary.
- The solution is then the linear superposition, ![]() ==
== ![]() +
+![]()
![]()
![]()
- The ![]() are determined via the boundary conditions (7.46).
are determined via the boundary conditions (7.46).
In practice, the torque M is given, not the rotation θ. We must find a relation θ(M), but also check that the stress field ![]() can be reduced to a couple (no resultant force). It is easy to show that the resultant of the shear stress is zero (Flügge p.121).
can be reduced to a couple (no resultant force). It is easy to show that the resultant of the shear stress is zero (Flügge p.121).
Since the shear stresses ![]() have no resultant, M is their moment with respect to any point O in the plane of the cross section.
have no resultant, M is their moment with respect to any point O in the plane of the cross section.
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() is the change of Φ along the one equipotential of Φ and hence is zero.
is the change of Φ along the one equipotential of Φ and hence is zero. ![]()
![]() is the change of Φ across the strip. Therefore,
is the change of Φ across the strip. Therefore,
![]()
![]()
![[Graphics:HTMLFiles/index_528.gif]](HTMLFiles/index_528.gif)
![]()
Fig. 7.5 Torsion bar, lines Φ = const in the cross section.
showing that the shear vector is along the lines Φ = const. The moment with respect to O, is
![]()
![]()
\!\(\* StyleBox[\"r\",
FontSize->16]\)\!\(\* StyleBox[\"×\",
FontSize->16]\)\!\(\* StyleBox[\"ds\",
FontSize->16]\) is twice the surface in green in the figure 7.5, times ![]() . The sum of all the moments is then 2B dΦ, B being the area inside the curve Φ = const, and dM = 2B dΦ is twice the volume of a horizontal slice of the stress hill of thickness dΦ.
. The sum of all the moments is then 2B dΦ, B being the area inside the curve Φ = const, and dM = 2B dΦ is twice the volume of a horizontal slice of the stress hill of thickness dΦ.
![]()
![]()
We can now solve (7.41), assuming a value for θ, and then calculating M from (7.47).
Plates
![[Graphics:HTMLFiles/index_535.gif]](HTMLFiles/index_535.gif)
Figure 7.6 Section through a plate before and after deformation.
We consider now a thin plane sheet of elastic material undergoing a deflection normal to its middle plane. The notations (![]() in the plane and
in the plane and ![]() = z, along
= z, along ![]() normal to the plane).
normal to the plane).
Figure 7.6 shows a section through the plate before and after deformation. The ![]() axis lies in the middle plane, and AB is a normal to it. When a load is applied, A moves to
axis lies in the middle plane, and AB is a normal to it. When a load is applied, A moves to ![]() , by an amount w (w = -
, by an amount w (w = - ![]() ). The line element AC becomes
). The line element AC becomes ![]()
![]() which is no longer horizontal, and AB becomes
which is no longer horizontal, and AB becomes ![]()
![]() no longer vertical. In thin plates, the shear strain is small enough to be neglected : the plate theory is built on the assumption of the conservation of normals.
no longer vertical. In thin plates, the shear strain is small enough to be neglected : the plate theory is built on the assumption of the conservation of normals.
The shear strain between a normal and the middle plane has two components :
![]()
![]()
When this is equal to zero, and since ![]() = w, we have
= w, we have
![]()
![]()
Integration gives,
![]()
![]()
The strain parallel to the middle plane is then,
![(*7.48*)ResultFrame[res748 = res = res71/.ud[i_] →CovariantD[Tensor[w], i] Tensor[z]/.CovariantD[Tensor[z], α_] →0//SymmetricStandardOrder[w]]](HTMLFiles/index_553.gif)
![]()
The strains are proportional to z and hence the stresses, which can be combined in each section to form a couple.
We calculate now these internal moments.
![]()
![]()
![]()
![[Graphics:HTMLFiles/index_558.gif]](HTMLFiles/index_558.gif)
Figure 7.7 Section through a plate.
In the area element of height h (see figure 7.7) we define a subelement (in green) of height dz. The green area is represented by the vector dA,
![]()
![]()
![]()
![]()
In this subelement, there is a force
![]()
![]()
Using (4.1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The sum of all the vertical components ![]()
![]() gives the shear force of the plate,
gives the shear force of the plate,

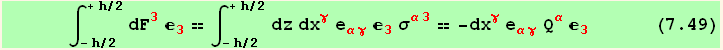
while the sum of all the in-plane components ![]()
![]() gives,
gives,

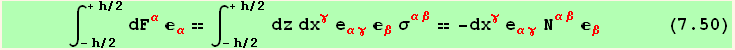
The moment of dF with respect to the center of the section is,

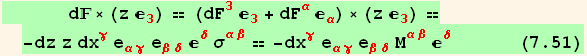
where we used the definitions of the stress resultants, the (transverse) shear force Q, the tension and shear tensor N, and the moment tensor M,
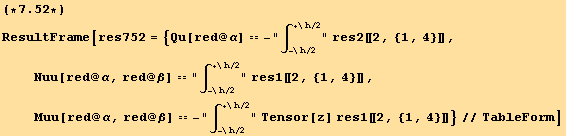
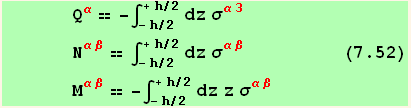
![[Graphics:HTMLFiles/index_584.gif]](HTMLFiles/index_584.gif)
Figure 7.8 Moments acting on a plate element.
For the line element AB in figure 7.8, we have ![]() =0and the last term in (7.51) reduces to
=0and the last term in (7.51) reduces to
![]()

![]()
For instance, ![]() ==
==![]() ==
==![]() is the bending moment acting on a cartesian plate element around the y axis,
is the bending moment acting on a cartesian plate element around the y axis, ![]() ==
==![]() the twisting moment around the x axis. We can do the same operations for the sides BC, CD, and DA, and obtain all the moments shown in figure 7.8.
the twisting moment around the x axis. We can do the same operations for the sides BC, CD, and DA, and obtain all the moments shown in figure 7.8.
The shear stress components are the components of the vector Q lying in the middle plane of the plate,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
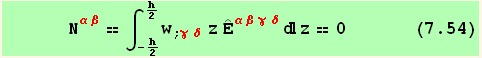
![]()
![]()
![]()
![]()
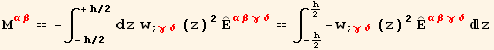
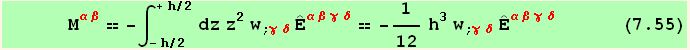
We see with (7.53) that ![]() do not play any role. Equation (7.54) might be called the elastic law of the plate.
do not play any role. Equation (7.54) might be called the elastic law of the plate.
Case of isotropic plates
We use equation (7.21)
![]()
![]()
![]()
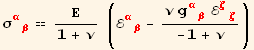
![]()
![]()
![]()
![]()
![]()
![]()
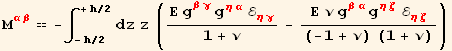
![]()
![]()
![]()
We have used the following definition for K, called the bending stiffness of the plate,
![]()
![]()
No similar relation can be found for Q==![]()
![]() as we have assumed the conservation of normals (no shear deformation)
as we have assumed the conservation of normals (no shear deformation)
Equilibrium of a plate element
We start from equation (6.5) splitted into j = β, and j = 3,
1) for i = α
![]()
![]()
![]()
![]()
![]()
and we notice that (using the results for the Christoffel symbols shown at the beginning of this chapter),
![]()
![]()
![]()
![]()
![]()
![]()
![]()
and multiply by z dz, and integrate,
![]()
![]()
in which, integrating by parts,
![]()
![]()
so that,
![]()
![]()
The second term ![]() is the moment of the shear stress
is the moment of the shear stress ![]() , and the third term \!\(∫\_\(\(-h\)/2\)\%\(\(+h\)/2\)\) dz z
, and the third term \!\(∫\_\(\(-h\)/2\)\%\(\(+h\)/2\)\) dz z ![]() is the moment of the volume forces acting on the plate material. Their sum is the external moment
is the moment of the volume forces acting on the plate material. Their sum is the external moment ![]() per unit area of the middle surface. With (7.52) the fourth term is
per unit area of the middle surface. With (7.52) the fourth term is ![]() , and the first term -
, and the first term -![]() .
.
The moment equilibrium of the plate element is finally,
![(res/.res[[2]] + res[[3]] →mu[red @ α]/.{res[[4]] →Qu[red @ α], res[[1]] → -CovariantD[Muu[red @ α, red @ β], red @ β]}) == 0<br />(*7.57*)](HTMLFiles/index_653.gif)
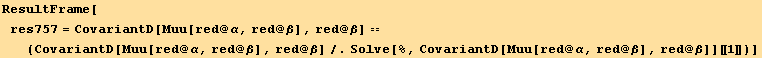
![]()
![]()
1) for i = 3
![]()
![]()
we multiply by dz and integrate,
![]()
![]()
![]()
![]()
![]()
![]()
where ![]() is the sum of the normal surface tractions
is the sum of the normal surface tractions ![]() and volume forces \!\(∫\_\(\(-h\)/2\)\%\(\(+h\)/2\)\) dz
and volume forces \!\(∫\_\(\(-h\)/2\)\%\(\(+h\)/2\)\) dz ![]() .
.
Equations (7.57) and (7.58) are the equilibrium conditions of the plate element. Together with equation (7.55) or (7.56) they give the 2+1+3=6 equations for the three moments ![]() , the two shear forces
, the two shear forces ![]() and the deflection w.
and the deflection w.
These equations can be condensed into a unique differential equation for the deflection w.
We differentiate (7.57) with respect to ![]() and replace
and replace ![]() from (7.58),
from (7.58),
![]()
![]()
then we express ![]() in terms of w via (7.55)
in terms of w via (7.55)
![res1 = res/.res755[[1]] →res755[[3]] ; (*7.59*)](HTMLFiles/index_675.gif)
![ResultFrame[res759 = Times[-1, #] &/@(res1/.{CovariantD[Êuuuu[i_, j_, k_, l_], m_] →0, CovariantD[Êuuuu[i_, j_, k_, l_], {m_, n_}] →0}//SymmetricStandardOrder[w])]](HTMLFiles/index_676.gif)
![]()
and in the isotropic case, using (7.56),
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| Created by Mathematica (November 27, 2007) |