8. Geometry of Curved Surfaces
Initialization
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Notation of the 2d and 3d litteral indices :
Latin characters are used for 3d, greek characters are use for 2d spaces.
Then SymbolSpaceDimension[index] gives the dimension of the space concerned by index.
SymbolSpaceDimension[Symbol] gives the
![]()
![]()
![]()
![]()
![]()
![Print[General surface (z≠0)]](HTMLFiles/index_24.gif)
![]()
![Print[Middle surface (z = 0)]](HTMLFiles/index_26.gif)
![]()
![]()
| e | basis symbol |
| g | metric tensor |
| permutation tensor | |
| Christoffel symbol | |
| η | Strain tensor |
| basis deformed symbol |
![]()
| a | basis symbol |
| a | metric tensor |
| e | permutation tensor |
| Γ | Christoffel symbol |
| E | Strain tensor |
| basis deformed symbol |
![]()
![]()
![]()
The red basis is here a monoclinic basis :
![]()
![]()
![]()
![]()
![]()
![]()
Metric and Curvature
In shell theory we shall consider points located on a certain curved surface, called middle surface, and its immediate vicinity. We use a coordinate system consisting of two curvilinear coordinates ![]() on that middle surface and the normal distance
on that middle surface and the normal distance ![]() from it.
from it.
We shall be interested in comparing quantities defined for points of the middle surface, that is, as functions of ![]() , with quantities defined for another surface at a small, constant distance z from it. It is then convenient to use two different notations, one for the middle surface
, with quantities defined for another surface at a small, constant distance z from it. It is then convenient to use two different notations, one for the middle surface ![]() = 0 and another for the generic surface
= 0 and another for the generic surface
![]() = z = const, as showb in the following,
= z = const, as showb in the following,
Notations : Deformation vectors : u for the middle surface (z = 0), v for the general surface (z ≠ 0).
The red basis is for the general surface z ≠ 0, the red basis for the middle surface z = 0 :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The basis vectors in the 2d surfaces are related to the position vectors s and r, with coordinates s = {![]() ,
, ![]() ,
, ![]() = 0} and r = {
= 0} and r = {![]() ,
, ![]() ,
, ![]() = z}
= z}
![]()
![]()
![]()
![]()
The metric tensor ![]() =
=![]() .
.![]() is written,
is written,
![]()
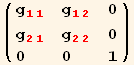
![]()
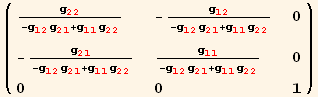
In this monoclinic basis, Christoffel symbols are simplified.![]() (Γb) is the symbol used for the Christoffel symbols in the general surface (z ≠ 0) and : Γ==
(Γb) is the symbol used for the Christoffel symbols in the general surface (z ≠ 0) and : Γ==![]() (z=0)
(z=0)
![]()
![]()
Note that here, due to the presence of curvature, the simplifications are less extended than in chapter 7.
DeclareBaseIndices[Base2d];
ed[red[α]].ed[red[3]]==0
PartialD[%[[1]],red[β]]==0
%//BasisDerivation[Γb,red@m][{e,red@α},red@β]//BasisDerivation[Γb,red@m][{e,red@3},red@β]
%//EvaluateDotProducts[e, g]
res1=%[[1]];
(* and equivalently *)
ed[red[β]].ed[red[3]]==0
PartialD[%[[1]],red[α]]==0
%//BasisDerivation[Γb,red@m][{e,red@β},red@α]//BasisDerivation[Γb,red@m][{e,red@3},red@α]
%//EvaluateDotProducts[e, g]
res2=%[[1]];
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Taking into account the symmetries of the Christoffel symbol :
Reminder : in the present notation, the two last indices are symmetrical, while the first is the tensorial index (the notation in Flügge's book is different)

![]()
![]()
![]()
ed[red[3]].ed[red[3]]==1
PartialD[%[[1]],red[α]]/2==0
%//BasisDerivation[Γb,red@m][{e,red@3},red@α]
Print[" which gives:"]; res1=%//EvaluateDotProducts[e, g]
Print[" and,"]
res2=(res1[[1]]//SymmetrizeSlots[])==0
Print[" while,"]
ed[red[α]].ed[red[3]]==0
PartialD[%[[1]],red[3]]==0
%//BasisDerivation[Γb,red@m][{e,red@α},red@3]//BasisDerivation[Γb,red@m][{e,red@3},red@3]
%//EvaluateDotProducts[e, g]
res3=%[[1]];
Print[" or,"]
res4=(res3/.res2[[1]]→0)==0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Taking into account the symmetry of the indices,
![(*8.2*)ResultFrame[res82 = 0 == res1[[1]] == res2[[1]] == res3[[1]] == res4[[1]]]](HTMLFiles/index_103.gif)
![]()
(*8.3*)
PartialD[ed[red[3]].ed[red[3]],red[3]]/2 == 0
%//BasisDerivation[Γb,red@m][{e,red@3},red@3]
ResultFrame[
res83=%//EvaluateDotProducts[e, g]]
![]()
![]()
![]()
DeclareBaseIndices[Base3d];
eu[red[3]].eu[red[3]]==0
PartialD[-%[[1]],red[α]]/2==0
%//BasisDerivation[Γb,red@m][{e,red@3},red@α]
%//EvaluateDotProducts[e, g, False];
res=(%//EinsteinSum[])/.TensorValueRules[g]
![]()
![]()
![]()
![]()
![(*8.4*)ResultFrame[res84 = res[[1]] == (res[[1]]//SymmetrizeSlots[]) == 0]](HTMLFiles/index_112.gif)
![]()
(*8.5*)
eu[red[3]].eu[red[3]]==0
PartialD[-%[[1]],red[3]]/2==0
%//BasisDerivation[Γb,red@m][{e,red@α},red@3]//BasisDerivation[Γb,red@m][{e,red@3},red@3]
%//EvaluateDotProducts[e, g, False]
ResultFrame[res85=(%//EinsteinSum[])/.TensorValueRules[g]]
![]()
![]()
![]()
![]()
![]()
To summarize :

In addition, because the metric tensor has the form (
),
![]()
![]()
0
![]()
![]()
0
0
0
1

![]()
We can now introduce these results in equations (5.2) and (5.3)

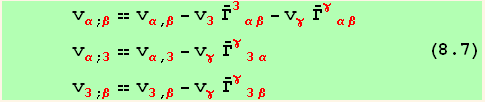

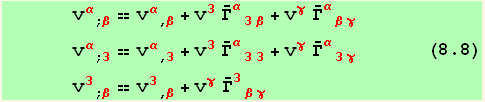
Restriction to the plane z = 0. The basis vectors in the tangent plane are now a = e( z = 0 )
Line element in the surface :
![]()
![]()
![]()
![]()
The normal vector ![]() being a unit vector has a direction which depends on
being a unit vector has a direction which depends on ![]() :
:
![]()
![]()
and,
![]()
![]()
![]()
![]()
The ![]() are the covariant components of the plane tensor, called the curvature tensor of the surface.
are the covariant components of the plane tensor, called the curvature tensor of the surface.
If we differentiate ![]() .
.![]() == 0,
== 0,
![]()
![]()
![]()
![]()
Using the result that the covariant derivative of the basis vector ![]() is zero, in the z=0 plane :
is zero, in the z=0 plane :

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()



![]()
![]()
![]()
![]()
To summarize :

We can also introduce the mixed and contravariant components,
![]()
![]()
![]()
so that, from (8.12),

![]()
and from (8.9),
![(*8.14*)ResultFrame[res814 = res89//UpDownSwap[red @ β]]](HTMLFiles/index_172.gif)
![]()
Infinitesimal displacement of the normal vector ![]()
![]()
![]()
and,

![]()
Note : In differential geometry, the coefficients ![]() ,
, ![]() =
= ![]() ,
, ![]() are respectively denoted E, F, G.
are respectively denoted E, F, G.
If we suppose that we make an infinitesimal displacement ![]()
![]() along
along ![]() , and that only
, and that only ![]() is nonzero, then
is nonzero, then ![]() is given by,
is given by,
![]()
![]()
![[Graphics:HTMLFiles/index_190.gif]](HTMLFiles/index_190.gif)
![[Graphics:HTMLFiles/index_191.gif]](HTMLFiles/index_191.gif)
Figure 8.2 Visualization of the curvature components..
As | ![]() | = 1, |
| = 1, | ![]() | is equal to the angle dφ of rotation of the normal from A to B, along
| is equal to the angle dφ of rotation of the normal from A to B, along ![]() .
.
The curvature of the surface in this direction is then given by (see figure (8.2a)),
![]()
If we suppose now that we make an infinitesimal displacement ![]()
![]() along
along ![]() , and that only
, and that only ![]() is nonzero, then
is nonzero, then ![]() is given by,
is given by,
![]()
![]()
As shown in figure (8.2b), ![]() corresponds to the twist of the surface :
corresponds to the twist of the surface :
![]()
and if {![]() }={
}={![]() }, then {
}, then {![]() }={
}={![]() } is equal to the twist. If {
} is equal to the twist. If {![]() }≠{
}≠{![]() }, then
}, then ![]() =
=![]() is equal to the twist.
is equal to the twist.
![]()
Scalar invariants
![]()
There are two such invariants :
The mean curvature :
![(*8.15*)ResultFrame[res815 = bud[red @ α, red @ α] == (bud[red @ α, red @ α]//EinsteinSum[]) ]](HTMLFiles/index_215.gif)
![]()
The Gaussian curvature :
It corresponds to the determinant b = det[![]() ], or in a tensorial invariant form,
], or in a tensorial invariant form,
![]()
![%//FullLeviCivitaExpand[e, g]//Expand//KroneckerAbsorb[g] (*8.16*)](HTMLFiles/index_219.gif)
![ResultFrame[res816 = Tensor[red @ b] == (bred$ = %//SumExpansion[{red @ β, red @ δ, red @ α, red @ γ}, {1, 2}]) ]](HTMLFiles/index_220.gif)
![]()
![]()
![]()
Tensor[red[b]] == -bud[red[1], red[2]] bud[red[2], red[1]]+bud[red[1],red[1]] bud[red[2], red[2]]
![]()
We can of course construct another invariant, but it is not independent of the others :
![]()
![]()
![]()
![]()
![]()
![]() is equal to
is equal to ![]() - 2b :
- 2b :
![]()
![]()
Covariant Derivative
In chapter 5, we have recalled the notion of covariant derivatives. Now we want to separate the behavior on the surfaces from its three dimensional behavior.
![]()
![]()
![]()
![]()
![]()
Using (5.7) where we derive with respect to ![]() , and (5.3),
, and (5.3),
![]()
(*8.17*)
ResultFrame[
res817=CovariantD[Tensor["u"],red[β]]==(res=CovariantD[ud[red@i],red@β] au[red@i])==(res//PartialSum[red@3,{red@α}])
]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Using the above conditions on the Christoffel symbols, we have the rules :
![]()
![]()
![]()
![]()
Similarly to the three dimensional case, we define a covariant derivative on the surface,
Notation for the two dimensional covariant derivative : CovariantD2d[expr, k], the derivative of ![]() , is noted
, is noted ![]() .
.
![]()
![]()
so that the first covariant derivatives are,
![(*8.18*)ResultFrame[res818 = {ruled1, ruled2d = ruled2/.Cd2dRule}//TableForm]](HTMLFiles/index_256.gif)
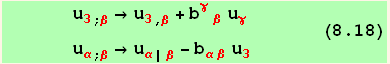
Equation (8.17) may then be written,
![]()
![ResultFrame[res819 = res[[1]] == (res[[3]]/.γ→α//ExpandCovariantD2d[labs0, red @ γ]//PartialDToDif//SymmetrizeSlots[]//Simplify)]](HTMLFiles/index_259.gif)
![]()
![]()
In a similar manner, the covariant derivative of ![]() gives (
gives ( ![]() =
= ![]() ),
),
![(*8.2*)ResultFrame[res820 = ruled2d//RaiseIndex[red @ α, red @ α]//RaiseIndex[red @ 3, red @ 3]//SymmetrizeSlots[] ]](HTMLFiles/index_265.gif)
![]()
Similarly we would find,
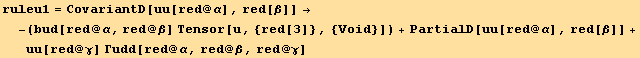
![]()
![]()
![]()
leading to an alternative form for (8.19)
![]()
![]()
![(CovariantD[Tensor[""], red[β]] == (res = CovariantD[uu[red @ i], red @ β] d[red @ i]) == (res//PartialSum[red @ 3, {red @ α}])/.res820) (*8.21*)](HTMLFiles/index_273.gif)
![ResultFrame[res821 = CovariantD[Tensor[""], red[β]] == ((res//PartialSum[red @ 3, {red @ α}])/.ruleu1/.ruleu2)]](HTMLFiles/index_274.gif)
![]()
![]()
For points in the vicinity of the middle surface, we can consider a derivative ![]()

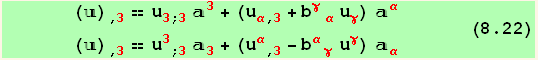
In the case when u is a plane vector (![]() = 0) covariant derivatives in 2d and in 3d become identical ( ; ≡ | ), while (8.21 becomes) :
= 0) covariant derivatives in 2d and in 3d become identical ( ; ≡ | ), while (8.21 becomes) :

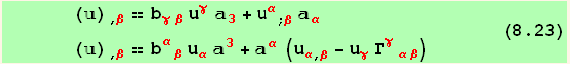
Similar formula can be derived for tensors. For example with a tensor ![]() , for which we restrict ourself to plane tensor
, for which we restrict ourself to plane tensor ![]() =
= ![]() =
= ![]() = 0,
= 0,
![]()
![]()
Note : ExpandCovariantD does not accept particular components (here i = 3), so that we have to work with arbitrary i , and then to particularize to i → 3:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
while,
![]()
![]()
and the second covariant derivatives are,
These results can be used when calculating the second derivatives of the basis vectors ![]() . From (8.11)
. From (8.11)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The last expression is also equal to ![]()
![]()
![]()
![]()
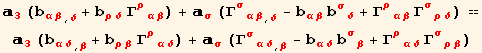
![]()
![]()
Using the explicit expression for the derivative of a tensor (obtained above),
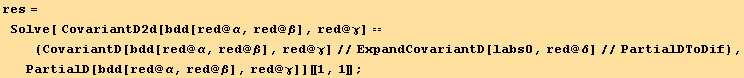
![]()
![]()
![(*8.24*)ResultFrame[ (res824 = {res = (res3/.ruleb//SymmetrizeSlots[]//SumExpansion[red @ μ, red @ ρ]//FullSimplify), (RaiseIndex[red @ α, red @ α]/@res)})//TableForm]](HTMLFiles/index_319.gif)
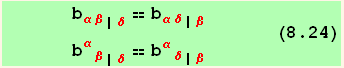
These equalities are two tensorial forms of the Gauss-Codazzi relations in differential geometry.
![]()
![]()
![]()
which contains a Riemann-Christoffel symbol defined by the following rule (see equation (5.6)),
RCrule[red@α_,red@β_,red@σ_,red@δ_,red@ρ_] :=
Γudd[red@ρ,red@α,red@β]Γudd[red@σ,red@δ,red@ρ]-Γudd[red@ρ,red@α,red@δ]*Γudd[red@σ,red@β,red@ρ]-PartialD[Γudd[red@σ,red@α,red@δ],red@β]+PartialD[Γudd[red@σ,red@α,red@β],red@δ] → Ruddd[red@σ,red@α,red@δ,red@β]

![ResultFrame[res825 = {resu = %[[1, 3]] == ( %[[1, 3]]/.Solve[%, %[[1, 3]]][[1]]), <br />resd = resu//LowerIndex[red @ δ, red @ δ]}//TableForm]](HTMLFiles/index_325.gif)
![]()
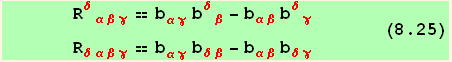
We can simplify even more the last formula
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Using the identity,
![]()
![]()
we find
![(*8.26*)ResultFrame[res826 = res/.rule//MetricSimplify[a] ]](HTMLFiles/index_338.gif)
![]()
At this step, we can introduce the Gaussian curvature b via the following equality,
![]()
![]()
Verification of this relation, by expanding the terms :
![]()
![]()
![]()
![]()
so that (8.26) ![]() ==-
==-![]()
![]()
![]()
![]() becomes,
becomes,

![]()
Equation (8.27) shows immediately all the symmetries of the 2d Riemann-Christoffel symbol : Antisymmetry with respect to the two first and between the two last symbols, symmetry between the two first and the two last symbols.
If ![]() ≠ 0, then
≠ 0, then ![]() ≠
≠ ![]() , and we can calculate the difference :
, and we can calculate the difference :
For "normal" tensors, the partial derivatives commute :
![]()
![]()
![]()
![res = %%[[1]] - %[[1]] == ( %%[[2]] - %[[2]]//SymmetricStandardOrder[Γ, {2, 3}]//SymmetricStandardOrder[u, {2, 3}]//FullSimplify)](HTMLFiles/index_359.gif)
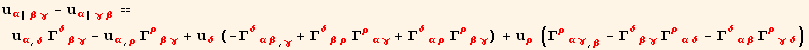
Using the definition of the Riemann-Christoffel symbol and relation (8.26),
![]()

![]()
![]()
In the next chapter, we shall need a similar relation for the second derivative of a symmetric, two dimensional tensor ![]() .
.

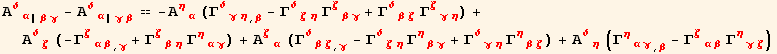

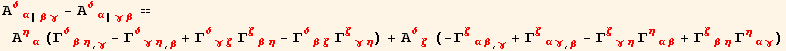
![]()
![]()
| Created by Mathematica (November 27, 2007) |