11. Principal Axis and Invariants

Initialization

Principal Direction

We look to area elements such that the force == acting on it is normal to the element. This means that the covariant components of the force

A non-trivial solution exists if,

This equation has three eigenvalues (one is necessarily real, but the other two may be either real or complex conjugate) ={,,}associated to three area elements =={,,}

Unsymmetric tensor

If we consider a general second-order tensor t,

or

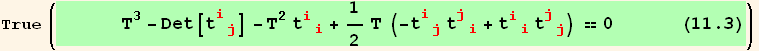
which is called the characteristic equation of the tensor t. If we change the frame , the three eigenvalues of (12.2) remain unchanged. This suppose that the coefficients are themselves invariants. Hence we have here three invariants built with t :

The invariants  tI,tII, and   tIII are respectively of order 1, 2 and  3 in t.  All combinaitions of  tI,tII, and   tIII are also invariants. An important invariant of degree 2 is 2 -3 tII, which can be expressed simply as a function of the zero trace tensor .

Proof :

For a symmetrical tensor t the eigenvectors and associated to two different eigenvalues and are orthogonal. We write

Tensor[t, {red[i], Void}, {Void, red[j]}]*Tensor[Subscript[v,"(m)"], {Void},
   {red[i]}] == Subscript[T,"(m)"]*Tensor[Subscript[v,"(m)"], {Void}, {red[j]}]
Tensor[t, {red[j], Void}, {Void, red[l]}]*Tensor[Subscript[v,"(n)"], {Void},
   {red[j]}] == Subscript[T,"(n)"]*Tensor[Subscript[v,"(n)"], {Void}, {red[l]}]

the second equation is multiplied by

and we multiply the first by , and the new (second) equation by

The left hand side are equal if and only if ==, that is to say if is symmetrical.

In this case the right hand side are equal and

if  m ≠ n. If the equation (11.2) has a double root, it is always possible to choose two orthogonal eigenvectors in the degenerate subspace. It can also be easily shown that all the eigenvalues of a symmetrical tensor must be real.

New base vectors

The eigenvectors orthogonal ,

can be chosen as a new base (blue for instance),

and we notice that their contravariant componentsare identical to the basis transformation .
From (12.5) we find,

In addition, the blue basis can be taken orthonormal, if we choose the eigenvectors as unit vectors :

The reference frame is cartesian. The tensor t is diagonal in this basis.

On the diagonal of the associated matrix, we have the eigenvalues .

Tensors of Stress and Strain

We come back to the area element with normal ,

pointing in the principal direction. The force is given by,

is the principal stress. It is a normal stress, root of

To a general stress field () corresponds its stress trajectories (tangent to the ) to which we can associate a curvilinear coordinate system .   

Two invariants σI and σII built as shown above, have already been encountered in chapter 4, equations (4.14),

and (4.21), using (12.4) for σ,

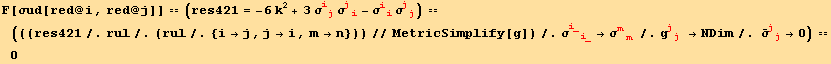
The strain tensor :
It is also a symmetric tensor which has three principal axis. From (4.11 or 12) applied to the reference frame , we see that in an isotropic elastic medium, the principal axis of stress and strain coincide.

Curvature

We have considered in Chapter 8, the curvature tensor , and its two invariants the mean curvature , and the Gaussian curvature {}(corresponding to the two invariants bI and bIII in the above notation). The invariant bII appears to be a combition of the two invariants bI and bIII .
is symmetrical, and has two orthogonal principal directions for which ====0. and are the principal curvatures. The lines of the curvature field are called the lines of principal curvature. They form an orthogonal set. This orthonormal set is not necessarily the best to use due to the boundary conditions which in general do not coincide with these lines.

Created by Mathematica  (November 27, 2007)