12. Compilation of Tensor Formulas

Initialization

e	basis symbol
g	metric tensor
	permutation tensor
	Christoffel symbol
η	strain tensor
	basis deformed symbol

a	basis symbol
a	metric tensor
e	permutation tensor
Γ	Christoffel symbol
E	strain tensor
	basis deformed symbol
	deformed metric tensor
	curvature deformed tensor

NB : The formulas written res... are essentially equivalent to the notation used in the preceding chapters. The first digit gives the chapter number, the others the order in the chapter. Of course only the final result is reported here, and the reader is invited to go to the corresponding chapter for details.
For convenience, here we have not introduced Tensor Shortcuts, but directly the interpreted outputs. This makes the formula particularly clear. To obtain explicit inputs, we only have to use "Convert to InputForm" in the menu  Cell, or to apply  resXXX//InputForm  to  resXXX.
Tensor Shorcuts have to be introduced by the reader when using specific formulas.

Important remark on the hidden structures :
Only the FullForm (or the InputForm) contains the whole information of the expressions.
Example :

Mathematical Formulas

Conventions

Basis

The various basis are distinguished by their flavor (black, red, blue, hat, star, tilde,...). The "black" basis is generally used for the orthornormal basis.

Base vectors and metric tensor

We mostly used to designate the basis vectors.
The associated metric tensor is ==.

Tensors

Notations :

Permutation pseudotensor symbol  ε    (ε is not a tensor! )

Our notations are different from that in Flügge's book.

Permutation or LeviCivita tensor  e

In a "red" basis (flavor = red), we note  flavor(g)==g==det()  

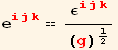
See also  PermutationPseudotensor, PermutationSymbolRule,  LeviCivitaOrder, LeviCivitaSimplify, FullLeviCivitaExpand,...

Coordinate transformation

A transformation from a "blue" basis to a "red" basis is written:

Determinants

Christoffel symbols

Notations of

and associated operators :

Symmetry :

or using :

Relation with the Metric Tensor :

Covariant derivatives

First derivatives

Note : Difference between general tensor and scalar tensors in some covariant derivations :

For a second order tensor

Second derivatives

Special tensor

Vector field operators

Gradient, Divergence, Curl, Laplacian

See TGrad, TDiv, TCurl, TLaplacian.

Integral theorems

Divergence theorem (Gauss' theorem) in three dimension:

circulation theorem (Stokes' theorem):

Curvature of a surface

is the curvature tensor   ( in differential geometry {,==,}, are denoted {E,F,G}).

Mean curvature

Gaussian curvature

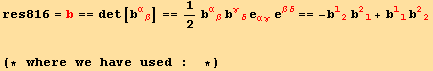
The are the basis vectors of the surface:

Covariant derivative on a curved surface

Here the "vertical bar" indicates the two-dimensional covariant derivative.

Gauss-Coddazzi equation

Riemann-Christoffel tensor (using res825 and res827)

Shell geometry

Note that the mixed metric tensors and are Krönecker delta.   z is the distance along the normal to the middle surface which is at z = 0.

Mechanical Formulas

Moment of a force

Strain

g is the metric tensor before deformation,  g the metric tensor after deformation.

Stress

Hooke's law, anisotropic material:

Elastic moduli, isotropic material:

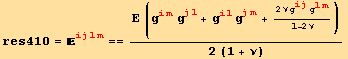
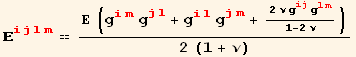
Lamé moduli:

Hooke's law, isotropic material:

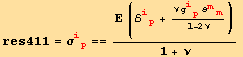
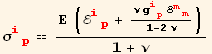
Elastic strain energy density (res44 and res419):

Dilatation energy ; distortion energy  

isotropic material:

Plasticity

yield condition:

flow law:

Viscous fluid, viscous volume change:

Kinematic relations

The strain tensor can be expressed as a function of the displacements :

Linearized expression:

General expression:

compatibility

Equilibrium

Newton's law

Fundamental equation of the theory of elasticity

anisotropic, homogeneous

isotropic

Elastic waves

In the following expressions,  Δ is the Laplacian.
For instance :

general:

dilatational wave:

shear wave:

Incompressible fluid

continuity equation

Navier-Stokes equation

invicid flow

Seepage flow

Darcy's law:

differential equation of the pressure field, general:

From  res631 and  res632:

differential equation of the pressure field, homogeneous medium:

gross stress

Plane strain

Hooke's law

fundamental equation

Airy stress function
definition:

where,

Airy stress function
differential equation:

Plane stress

Hooke's law

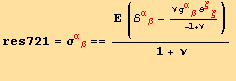
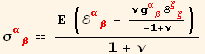
fundamental equation:

Airy stress function
differential equation:

Torsion

stress function

torque

Plates

elastic law:

differential equation

Shells

strains of the middle surface:

equilibrium

reduced equilibrium conditions

elastic law

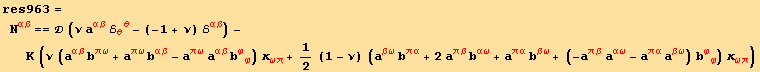
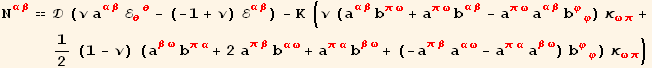
Buckling of a plate

Created by Mathematica  (November 27, 2007)