Gradient, Divergence, Curl, Laplacian
We give here as an example, the method to calculate the operators gradient, divergence, curl and laplacian in curvilinear coordinates.
We apply the method to the case of spherical coodinates, but the procedure is general.
Initialization
![]()
![]()
![]()
![]()
The flavors allow to distinguish between various basis.
The change of flavor is given by ToFlavor[new, old]. ToFlavor[bar] is equivalent to ToFlavor[bar, Identity].
![]()
![]()
Curvilinear Coordinates
![]()
![]()
We considera general basis with a red flavor :
![]()
![]()
![]()
![]()
where ![]() is a canonical orthonormal basis
is a canonical orthonormal basis
![]()
![]()
![]()
![]()
![]()
This red basis is completely determined by its metric tensor ![]()
![]()
![]()
Example : Spherical coordinates

![]()
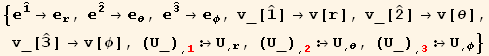
![CartesianToSpherical = {xu[1] →xu[red @ 1] Sin[xu[red @ 2]] Cos[xu[red @ 3]], xu[2] →xu[red @ 1] Sin[xu[red @ 2]] Sin[xu[red @ 3]], xu[3] →xu[red @ 1] Cos[xu[red @ 2]]} ;](HTMLFiles/index_25.gif)
![]()
![]()
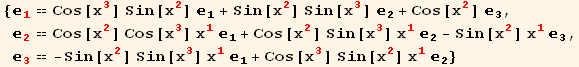
![]()
![]()


![]()
![]()
![g_ (ij)^(ij) == ( {{1, 0, 0}, {0, (x_1^1)^2, 0}, {0, 0, Sin[x_2^2]^2 (x_1^1)^2}} ) (A 1)](HTMLFiles/index_35.gif)
![]()
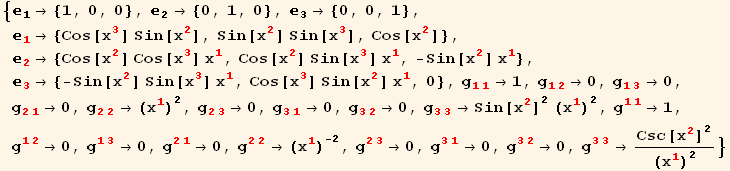
The red basis is generally not normalized (or even sometimes not orthonormal, and we must then first diagonalize g).
So we choose to define an orthonormal "hat" basis ( ![]() is the identity matrix) as follows :
is the identity matrix) as follows :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
and we have the relation, where ![]() is chosen the identity matrix,
is chosen the identity matrix,
![]()
![]()
![]()
this allows to calculate ![]() as the square root of
as the square root of ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![( {{1, 0, 0}, {0, (x_1^1)^2, 0}, {0, 0, Sin[x_2^2]^2 (x_1^1)^2}} )](HTMLFiles/index_61.gif)
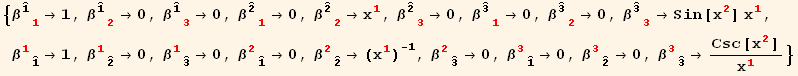
![( {{1, 0, 0}, {0, x_1^1, 0}, {0, 0, Sin[x_2^2] x_1^1}} )](HTMLFiles/index_63.gif)
We verify that this is correct :
![]()
![]()
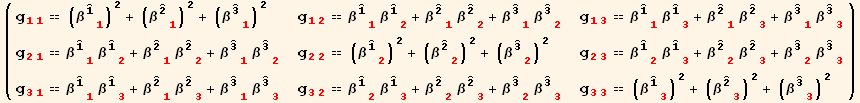

![]()
![]()
![]()
![]()
![]()
and we can check here that the hat basis is orthonormal and ![]() ==
==![]() ,
,
![]()
![g_ (Overscript[i,^] Overscript[j,^])^(Overscript[i,^] Overscript[j,^]) == ( {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}} )](HTMLFiles/index_82.gif)
Gradient of a potential
Gradient of a potential U in curvilinear coordinates :
![]()
![]()
![]()
![]()
![]()
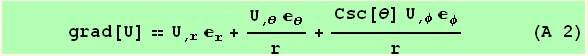
Curl of a vector
Curl of a vector V in curvilinear coordinates :
Let,
![]()
![]()
![]()
![]()
![]()
![]()
![curl[] == (v_j^j_ (; i) _k^k ε_ (ijk)^(ijk))/(g)^1/2](HTMLFiles/index_95.gif)
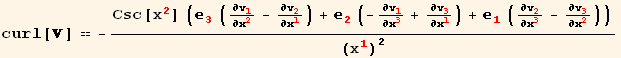
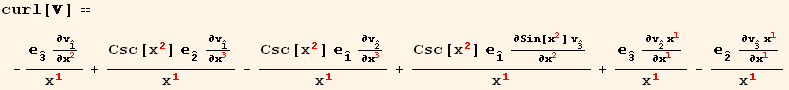
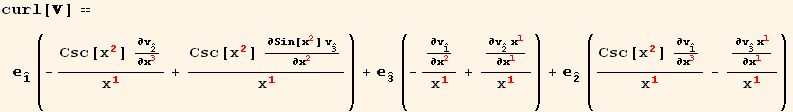
![ResultFrame[res[[1]] == Collect[(res[[2]]/.TensorValueRules[x]/.SphericalIndices), {d[r], d[θ], d[φ]}, Simplify]//PartialDToDif]](HTMLFiles/index_99.gif)
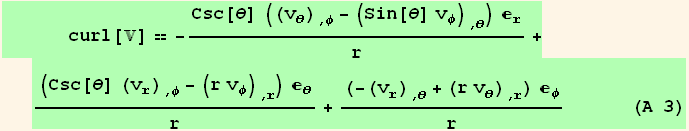
Divergence of a vector
Divergence of a vector in spherical coordinates :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Derivative of the determinant of the metric tensor :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
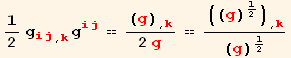
![]()
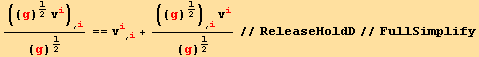
![div[] == v_i^i_ (, i) + (((g)^1/2) _ (, i) v_i^i)/(g)^1/2](HTMLFiles/index_131.gif)
![]()
![ResultFrame["div[]" == HoldOp[PartialD][PartialD[(g)^1/2 v_i^i, red @ i]]/(g)^1/2]](HTMLFiles/index_133.gif)
![div[] == ((g)^1/2 v_i^i) _ (, i)/(g)^1/2 (A 4)](HTMLFiles/index_134.gif)
Volume element ![]() :
:
![]()
![]()
![]()
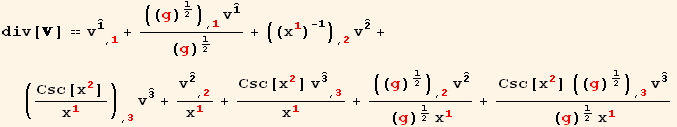
![res = res0/.Tensor[red @ g]^(1/2) →vol/.(1/Tensor[red @ g]^(1/2) →1/vol)//DifToPartialD[{x, δ, g, Γ}]//UnnestTensor//Kronecker[δ]//PartialDSimplify](HTMLFiles/index_140.gif)
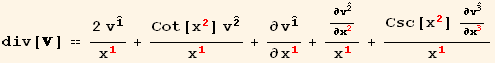

![]()
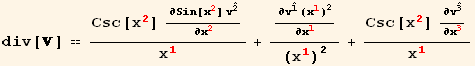
![]()
![]()
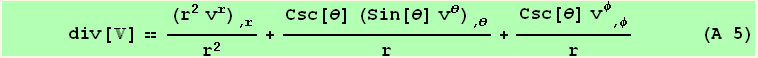
Laplacian of a scalar field
Laplacian of a scalar field in spherical coordinates :
![]()
![]()
![]()
![]()
Or also from the expression (A 11) of the divergence,
![]()
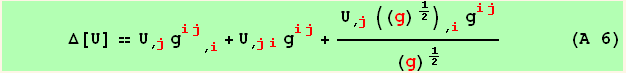

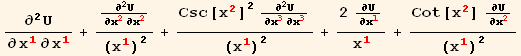
Which can also be written in a more compact form :
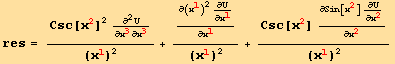
![]()
![(Csc[x_2^2]^2 ∂^2U/∂x_3^3∂x_3^3)/(x_1^1)^2 + ∂ (x_1^1)^2 ∂U/∂x_1^1/∂x_1^1/(x_1^1)^2 + (Csc[x_2^2] ∂Sin[x_2^2] ∂U/∂x_2^2/∂x_2^2)/(x_1^1)^2](HTMLFiles/index_158.gif)
![]()
![]()
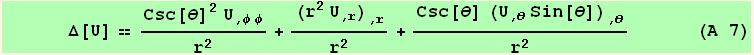
![]()
| Created by Mathematica (November 27, 2007) |