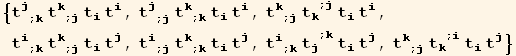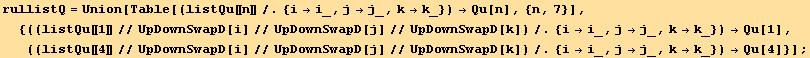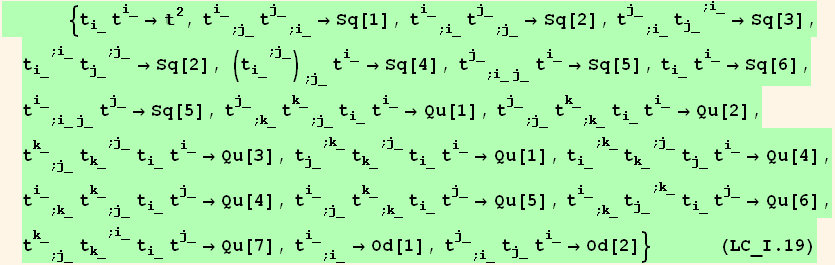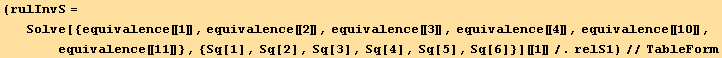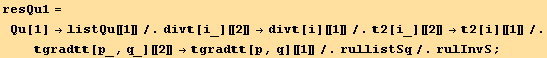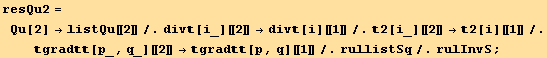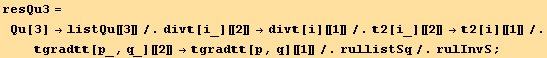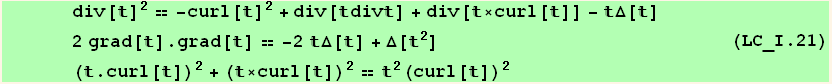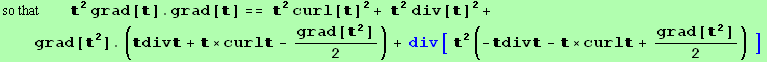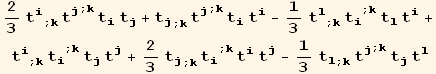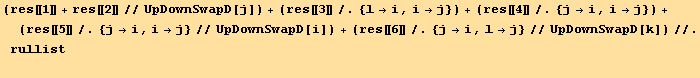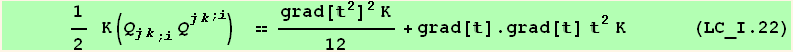Liquid Crystals
In this example, I apply Tensorial and TContinuumMechanics, to the case of distortions in a nematic single liquid crystal.
I first recall that in a nematic single crystal, the molecules are aligned on average along one common vector denoted t in the following. But the molecules are not oriented, so the direction ±t are equivalent.
The order parameter is a tensor, called Q which must be invariant by the change t⇔- t.
A nematic can be deformed, and these elastic deformations modify the free energy of the system. Three main deformations can be considered :
- the splay (where div t ≠ 0)
- the bend (where t . curl t = 0)
- the twist (where t // curl t)
This leads to introduce three elastic constants (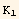 ,
, 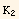 ,
, 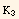 ).
).
A systematic way to found explicit relations between Q and t, curl t and div t, is described here.
Initialization
![Needs["TensorCalculus4`Tensorial`"]](HTMLFiles/index_4.gif)
![Needs["TContinuumMechanics2`TContinuumMechanics`"] <br />](HTMLFiles/index_5.gif)

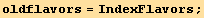

![DeclareIndexFlavor[{black, Black}, {red, Red}, {green, ForestGreen}, {star, SuperStar}, {blue, Blue}, {hat, OverHat}, {tilde, OverTilde}, {bar, OverBar}]](HTMLFiles/index_10.gif)
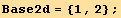
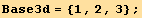
![DeclareBaseIndices[Base3d] ;](HTMLFiles/index_13.gif)
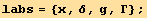
![SetScalarSingleCovariantD[False]](HTMLFiles/index_15.gif)
![DefineTensorShortcuts[{{, J, J1, J2, , t, x}, 1}, {{g, gt, Q, Q§, Β, β}, 2}, {{Γ}, 3}, {{}, 4}] ;](HTMLFiles/index_16.gif)
Conventionally, the "black" flavor is used for the canonical orthonormal basis :
![ = IdentityMatrix[3] ;](HTMLFiles/index_17.gif)
![SetTensorValues[guu[black @ i, black @ j], ]](HTMLFiles/index_18.gif)
![SetTensorValues[gud[black @ i, black @ j], ]](HTMLFiles/index_19.gif)
![SetTensorValues[gdu[black @ i, black @ j], ]](HTMLFiles/index_20.gif)
![SetTensorValues[gdd[black @ i, black @ j], ]](HTMLFiles/index_21.gif)
Nematics : Microscopic approach
Simple rods
The rods have in average the direction t.
A single rod is charaterized by a unit vector J in spherical coordinates. We will use the average direction t=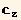 of the rods, as Z-axis:
of the rods, as Z-axis:
![ = d[Z] ;](HTMLFiles/index_23.gif)
![DeclareBaseIndices[{X, Y, Z}]](HTMLFiles/index_24.gif)
![SetTensorValues[gtud[black @ i, black @ j], ]](HTMLFiles/index_25.gif)
![SetTensorValues[gtdu[black @ i, black @ j], ]](HTMLFiles/index_26.gif)
![SetTensorValues[gtdd[black @ i, black @ j], ]](HTMLFiles/index_27.gif)
![comp = Ju[i]//EinsteinArray[]](HTMLFiles/index_28.gif)
![ = Ju[i] d[i]](HTMLFiles/index_29.gif)

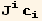
In spherical coordinates, the unit vector J is given by,

![BasisVectors = CoordinatesToCartesian[{1, θ, φ}, Spherical]](HTMLFiles/index_33.gif)
![SetTensorValueRules[Ju[i], BasisVectors]](HTMLFiles/index_34.gif)
![{Cos[φ] Sin[θ], Sin[θ] Sin[φ], Cos[θ]}](HTMLFiles/index_35.gif)
![MatrixForm/@(comp == (comp/.TensorValueRules[J]))](HTMLFiles/index_36.gif)
![( {{J_X^X}, {J_Y^Y}, {J_Z^Z}} ) == ( {{Cos[φ] Sin[θ]}, {Sin[θ] Sin[φ]}, {Cos[θ]}} )](HTMLFiles/index_37.gif)
Distribution function of the state of alignment of the rods:
![f[θ, φ] Ω ;](HTMLFiles/index_38.gif)
![(* with *) Ω == Sin[θ] θ φ ;](HTMLFiles/index_39.gif)
For nematics, f is (1) independent of φ, and (2) m and -m are equivalent so that f(θ)==f(π-θ)
![Average[X_] := <X> == ∫_0^(2π) (∫_0^π f[θ] X Sin[θ] θ) φ](HTMLFiles/index_40.gif)
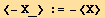
![Average[X_ + Y_] := <X + Y> == Average[X][[2]] + Average[Y][[2]]](HTMLFiles/index_42.gif)
![Average[1]/.f[θ_] →1/(4π)](HTMLFiles/index_43.gif)
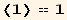
![Jt = ( . //EvaluateDotProducts[, gt]//EinsteinSum[])/.TensorValueRules[J]](HTMLFiles/index_45.gif)


![Average[Jt/.θ→π - θ]/.Integrate[F_, var_] :→Integrate[(F/.θ→π - θ), var]/.f[π - θ] →f[θ]](HTMLFiles/index_48.gif)
![<J_Z^Z> == 2 π ∫_0^πf[θ] Sin[θ] J_Z^Zθ](HTMLFiles/index_49.gif)
![<J_Z^Z> == 2 π ∫_0^πf[θ] Sin[θ] J_Z^Zθ](HTMLFiles/index_50.gif)
so that,
![Average[Jt][[1]] == 0](HTMLFiles/index_51.gif)
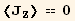
The first multipole which gives a non zero average is the quadrupole,
![M2[θ_] := (3Cos[θ]^2 - 1)/2](HTMLFiles/index_53.gif)
![Average[M2[θ]]](HTMLFiles/index_54.gif)
![Average[M2[θ]]/.f[θ_] →1/(4π) (* when f[θ] is peaked on a value θ_0 of θ : *)](HTMLFiles/index_55.gif)
![{M2[0], M2[π/2], M2[π]}](HTMLFiles/index_56.gif)
![<1/2 (-1 + 3 Cos[θ]^2) > == 2 π ∫_0^π1/4 (1 + 3 Cos[2 θ]) f[θ] Sin[θ] θ](HTMLFiles/index_57.gif)
![<1/2 (-1 + 3 Cos[θ]^2) > == 0](HTMLFiles/index_58.gif)
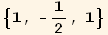
Order parameter Q: Three dimensional situation
![DeclareBaseIndices[Base3d] ;](HTMLFiles/index_60.gif)
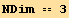
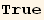
The system is located in an orthonormal (black) basis e, and we consider two molecules or fiber elements with principal axis 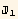 and
and 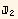 , close from one another. The principal axis may correspond to a magnetic moment, or to identify a steric constrain...
, close from one another. The principal axis may correspond to a magnetic moment, or to identify a steric constrain...
![_1 := J1u[i] d[i]](HTMLFiles/index_65.gif)
![_2 := J2u[j] d[j]](HTMLFiles/index_66.gif)
![ := tu[k] d[k]](HTMLFiles/index_67.gif)
The hamiltonian of interaction is,
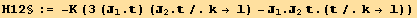
![H12 := 3K J1u[i] J2u[j] (Coefficient[H12§/(3K)//EvaluateDotProducts[, g, False], J1u[i] J2u[j]]//MetricSimplify[g])](HTMLFiles/index_69.gif)
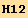
![%//Expand//UpDownSwap[black @ i]//Simplify](HTMLFiles/index_71.gif)
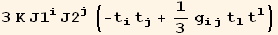
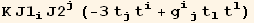
The uniaxial nematic tensor order parameter is (we can verify that its trace is zero) :
![Q§ud[i_, j_] := Tensor[t, {i}, {Void}] * Tensor[t, {Void}, {j}] + Rational[-1, 3] * Tensor[g, {i, Void}, {Void, j}] * Tensor[t, {l}, {Void}] * Tensor[t, {Void}, {l}]](HTMLFiles/index_74.gif)
![Q§ud[i, j]/.tu[k_] td[k_] →Abs[t]^2](HTMLFiles/index_75.gif)
![(Q§mat = (%//ArrayExpansion[black @ i, black @ j])//MetricSimplify[g])//MatrixForm](HTMLFiles/index_76.gif)
![-1/3 Abs[t]^2 g_ (ij)^(ij) + t_j^j t_i^i](HTMLFiles/index_77.gif)
![( {{-1/3 Abs[t]^2 + t_1^1 t_1^1, t_2^2 t_1^1, t_3^3 t_1^1}, {t_1^1 t_2^2, -1/3 Abs[t]^2 + t_2^2 t_2^2, t_3^3 t_2^2}, {t_1^1 t_3^3, t_2^2 t_3^3, -1/3 Abs[t]^2 + t_3^3 t_3^3}} )](HTMLFiles/index_78.gif)
It is convenient to introduce the usual parameter q by,
![Abs[t]^2 == NDim q/2](HTMLFiles/index_79.gif)
![Abs[t]^2 == (3 q)/2](HTMLFiles/index_80.gif)
![(Eigenvalues[Q§mat]//Simplify)/.(tu[k] td[k]//EinsteinSum[]) →Abs[t]^2](HTMLFiles/index_81.gif)
![Ev = %/.Abs[t]^2→NDim q/2](HTMLFiles/index_82.gif)
![Eigenvectors[Q§mat]//MatrixForm](HTMLFiles/index_83.gif)
![%[[1]] . %[[3]]/.{td[i_] →tu[i]}](HTMLFiles/index_84.gif)
![%%[[2]] . %%[[3]]/.{td[i_] →tu[i]}](HTMLFiles/index_85.gif)
![%%%[[1]] . %%%[[2]]/.{td[i_] →tu[i]}](HTMLFiles/index_86.gif)
![{-1/3 Abs[t]^2, -1/3 Abs[t]^2, (2 Abs[t]^2)/3}](HTMLFiles/index_87.gif)
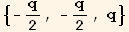
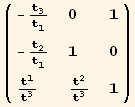
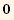
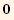
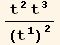
![diagQud[i_, j_] := 0](HTMLFiles/index_93.gif)
![diagQud[1, 1] := Ev[[1]]](HTMLFiles/index_94.gif)
![diagQud[2, 2] := Ev[[2]]](HTMLFiles/index_95.gif)
![diagQud[3, 3] := Ev[[3]]](HTMLFiles/index_96.gif)
![1 = (td[3] Eigenvectors[Q§mat][[1]] + td[2] Eigenvectors[Q§mat][[2]]) td[1]//Simplify](HTMLFiles/index_97.gif)
![2 = (-td[2] Eigenvectors[Q§mat][[1]] + td[3] Eigenvectors[Q§mat][[2]]) td[1]](HTMLFiles/index_98.gif)
![3 = Eigenvectors[Q§mat][[3]] td[3]/.tu[k_] →td[k]//Simplify](HTMLFiles/index_99.gif)
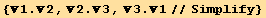
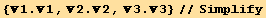
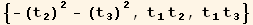
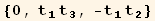
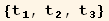
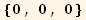
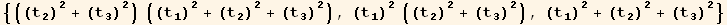
The red basis will be here a monoclinic basis :
![ResultFrame[Qud[i, j] == Q§ud[i, j]//ToFlavor[red]]](HTMLFiles/index_107.gif)

Rotation of the basis:
We recall first the expression of a rotation matrix using Euler angles (α, β, γ)
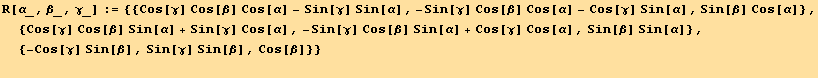
![R[α, β, γ]//MatrixForm](HTMLFiles/index_110.gif)

![R[α, β, γ]//Inverse//FullSimplify//MatrixForm](HTMLFiles/index_112.gif)
![% - (R[α, β, γ]//Transpose)//MatrixForm](HTMLFiles/index_113.gif)
![R[α, β, γ]//Det//FullSimplify](HTMLFiles/index_114.gif)
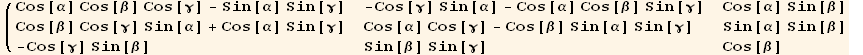

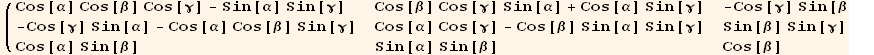
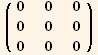
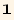
R is the product of the three rotations,
![R[α, β, γ] == R[α, 0, 0] . R[0, β, 0] . R[0, 0, γ]](HTMLFiles/index_120.gif)
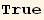
We call Β the basis change :
![SetTensorValueRules[Βud[j, red @ i], R[α, β, γ]]](HTMLFiles/index_122.gif)
![SetTensorValueRules[Βud[red @ i, j], R[α, β, γ]]](HTMLFiles/index_123.gif)
![TensorValueRules[Β]](HTMLFiles/index_124.gif)
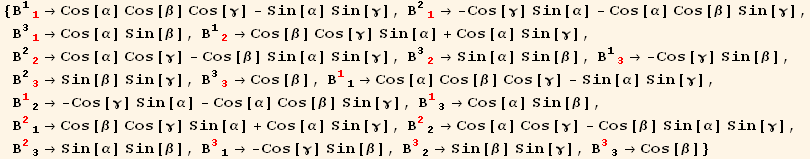
and check that,
![Βud[red @ i, j] Βud[j, red @ k]](HTMLFiles/index_126.gif)
![(%//EinsteinSum[]//ArrayExpansion[red @ i, red @ k])/.TensorValueRules[Β]//FullSimplify//MatrixForm](HTMLFiles/index_127.gif)

![Qud[red @ i, red @ j] == Q§ud[p, q] Βud[red @ i, p] Βud[q, red @ j]](HTMLFiles/index_130.gif)
![%//ExpandAll//KroneckerAbsorb[Β]](HTMLFiles/index_131.gif)
![Print["with in addition"]](HTMLFiles/index_132.gif)
![tu[l] td[l]//EinsteinSum[] ;](HTMLFiles/index_133.gif)
![% == (%/.{td[l_] →td[red @ i] Βud[red @ i, l], tu[l_] →tu[red @ j] Βud[l, red @ j]}//EinsteinSum[]) ;](HTMLFiles/index_134.gif)
![%/.TensorValueRules[Β]//FullSimplify](HTMLFiles/index_135.gif)
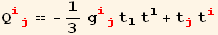

For a general rotation, we would have,
![Q§ud[red @ i_, red @ j_] := Q§ud[p, q] Βud[red @ i, p] Βud[q, red @ j]](HTMLFiles/index_140.gif)
![(Q§val = Q§ud[red @ i, red @ j]//EinsteinSum[]//ArrayExpansion[red @ i, red @ j]//MetricSimplify[g])//MatrixForm](HTMLFiles/index_141.gif)
![(Qval = Q§val/.TensorValueRules[Β]/.tu[k_] →td[k])//MatrixForm](HTMLFiles/index_142.gif)


t in the x-y plane (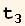 =0):
=0):
t makes an angle φ with the first axis 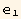 :
:
{td[1]→Abs[t] Cos[φ],td[2]→Abs[t] Sin[φ]}
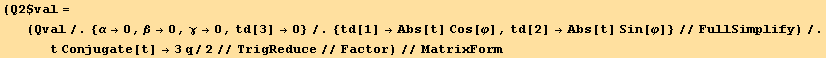
![( {{1/4 q (1 + 3 Cos[2 φ]), 3/4 q Sin[2 φ], 0}, {3/4 q Sin[2 φ], -1/4 q (-1 + 3 Cos[2 φ]), 0}, {0, 0, -q/2}} )](HTMLFiles/index_148.gif)
In a basis {X, Y, Z} :
![DeclareBaseIndices[{X, Y, Z}]](HTMLFiles/index_149.gif)
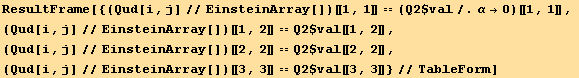
![DeclareBaseIndices[Base3d] ;](HTMLFiles/index_151.gif)
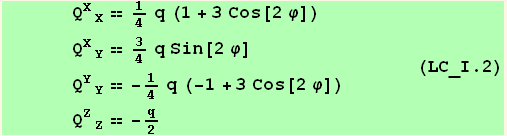
Free energy in terms of q and φ (one-dimensional)
"Tensorization" of the parameters : Tensor Notations
It is convenient in the following to use scalar tensors in place of the usual parameters. We will denote with an UnderBar the tensor associated with each parameter.
![Underscript[_, _] := Tensor[]](HTMLFiles/index_153.gif)
![Ruleφq = {φ→Underscript[φ, _], q→Underscript[q, _]} ; (* Replaces the parameters by tensors *)](HTMLFiles/index_154.gif)
![Qud[1, 1] == (Q2$val/.Ruleφq)[[1, 1]]](HTMLFiles/index_155.gif)
![Qud[1, 2] == (Q2$val/.Ruleφq)[[1, 2]]](HTMLFiles/index_156.gif)
![Qud[2, 2] == (Q2$val/.Ruleφq)[[2, 2]]](HTMLFiles/index_157.gif)
![Qud[3, 3] == (Q2$val/.Ruleφq)[[3, 3]]](HTMLFiles/index_158.gif)
![Q_ (11)^(11) == 1/4 (1 + 3 Cos[2 φ]) q](HTMLFiles/index_159.gif)
![Q_ (12)^(12) == 3/4 Sin[2 φ] q](HTMLFiles/index_160.gif)
![Q_ (22)^(22) == -1/4 (-1 + 3 Cos[2 φ]) q](HTMLFiles/index_161.gif)
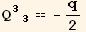

![QqφRule := Tensor[Q, {Void, Void}, {black @ i_, black @ j_}] :→Q2§val[[i, j]]](HTMLFiles/index_164.gif)
![( Q2§val/.Underscript[φ, _] →0)//MatrixForm](HTMLFiles/index_165.gif)
![( Q2§val/.Underscript[φ, _] →π/2)//MatrixForm](HTMLFiles/index_166.gif)
![-( Q2§val/.Underscript[φ, _] →π/2) - ( Q2§val/.Underscript[φ, _] →0)//MatrixForm](HTMLFiles/index_167.gif)
![2/3 (Underscript[q, _] - %)//MatrixForm](HTMLFiles/index_168.gif)


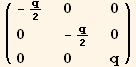
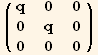
![2 = DiagonalMatrix[{1, 1, 0}] ; 2 = {{0, 1, 0}, {-1, 0, 0}, {0, 0, 0}} ;](HTMLFiles/index_173.gif)
A. Forms 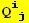
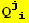 ,
, 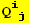
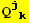
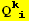 , ... and {
, ... and {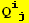 }, without derivatives
}, without derivatives
![2/3 (Qud[i, j] Qud[j, i])//StandardDownIndices[g]//EinsteinSum[] ;](HTMLFiles/index_180.gif)
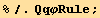
![resfQ2 = 2/3 (Qud[i, j] Qud[j, i]) == %//FullSimplify](HTMLFiles/index_182.gif)
![4/3 (Qud[i, j] Qud[j, k] Qud[k, i])//StandardDownIndices[g]//EinsteinSum[] ;](HTMLFiles/index_183.gif)
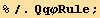
![resfQ3 = 4/3 (Qud[i, j] Qud[j, k] Qud[k, i]) == %//FullSimplify](HTMLFiles/index_185.gif)
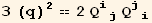
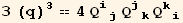
![resfQDet = Det[Qud[i, j]] == Det[Q2§val]//FullSimplify](HTMLFiles/index_188.gif)
![Qud[i, j] Qud[j, k] == (Q2§val . Q2§val//FullSimplify//MatrixForm)](HTMLFiles/index_189.gif)
![Qud[i, j] Qud[j, k] Qud[k, l] == (Q2§val . Q2§val . Q2§val//FullSimplify//MatrixForm)](HTMLFiles/index_190.gif)
![4 Det[Q_ (ij)^(ij)] == (q)^3](HTMLFiles/index_191.gif)
![Q_ (ij)^(ij) Q_ (jk)^(jk) == ( {{1/8 (5 + 3 Cos[2 φ]) (q)^2, 3/8 Sin[2 φ] (q)^2, 0}, {3/8 Sin[2 φ] (q)^2, 1/8 (5 - 3 Cos[2 φ]) (q)^2, 0}, {0, 0, (q)^2/4}} )](HTMLFiles/index_192.gif)
![Q_ (ij)^(ij) Q_ (jk)^(jk) Q_ (kl)^(kl) == ( {{1/16 (7 + 9 Cos[2 φ]) (q)^3, 9/16 Sin[2 φ] (q)^3, 0}, {9/16 Sin[2 φ] (q)^3, 1/16 (7 - 9 Cos[2 φ]) (q)^3, 0}, {0, 0, -(q)^3/8}} )](HTMLFiles/index_193.gif)
B. Forms with first order covariant derivatives
I. Forms 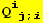
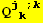
Warning : EinsteinSum[] does not works :
1) on contravariant derivatives (we apply StandardDownIndices[g]).
2) on expression in an hold form (we apply ReleaseHoldD).
![(CovariantD[Qud[i, j], i]) (ContravariantD[(Qud[j, k]/.l→h), k])](HTMLFiles/index_196.gif)
![%//StandardDownIndices[g]//ReleaseHoldD//EinsteinSum[] ;](HTMLFiles/index_197.gif)
![%/.CovariantD[Tensor[t__], i_] :→PartialD[labs][Tensor[t], xu[i]] ; (*the basis is orhonormal *)](HTMLFiles/index_198.gif)
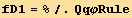
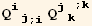
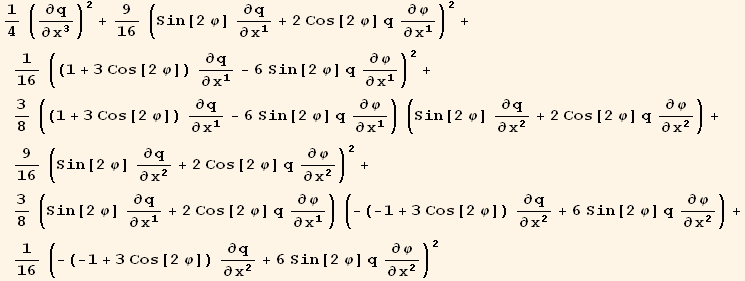
The coefficients of the partial derivatives 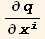 and
and 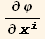 is given by,
is given by,

![(res1qq = Table[D[res1/2, PDq[i], PDq[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_205.gif)
![(res1qφ = Table[D[res1/2, PDq[i], PDφ[j]], {i, 3}, {j, 3}]//TrigReduce//Simplify)//MatrixForm](HTMLFiles/index_206.gif)
![(res1φφ = Table[D[res1/2, PDφ[i], PDφ[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_207.gif)
![( {{1/8 (5 + 3 Cos[2 φ]), 3/8 Sin[2 φ], 0}, {3/8 Sin[2 φ], 1/8 (5 - 3 Cos[2 φ]), 0}, {0, 0, 1/4}} )](HTMLFiles/index_208.gif)
![( {{-3/8 Sin[2 φ] q, 3/8 (3 + Cos[2 φ]) q, 0}, {3/8 (-3 + Cos[2 φ]) q, 3/8 Sin[2 φ] q, 0}, {0, 0, 0}} )](HTMLFiles/index_209.gif)

and we can check that they are equal to,
![res1qq == 1/Underscript[q, _]^2Q2§val . Q2§val//Simplify](HTMLFiles/index_211.gif)
![res1qφ == 1/4 D[Q2§val, Underscript[φ, _]] + 9/8Underscript[q, _] 2//Simplify](HTMLFiles/index_212.gif)
![res1φφ == 9/4Underscript[q, _]^22//Simplify](HTMLFiles/index_213.gif)

Introducing the projection 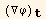 of ∇φ on the t-plane we find the expression for
of ∇φ on the t-plane we find the expression for 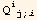
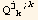 :
:


II. Forms 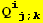
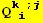
with a similar approach, we find
![CovariantD[Qud[i, j], k] ContravariantD[(Qud[k, i]/.l→h), j]](HTMLFiles/index_224.gif)
![%//StandardDownIndices[g]//ReleaseHoldD//EinsteinSum[] ;](HTMLFiles/index_225.gif)
![%/.CovariantD[Tensor[t__], i_] :→PartialD[labs][Tensor[t], xu[i]] ; (*the basis is orhonormal *)](HTMLFiles/index_226.gif)
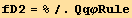
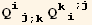
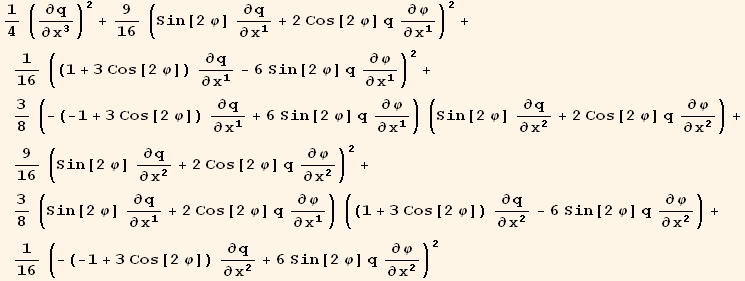

![(res2qq = Table[D[res2/2, PDq[i], PDq[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_231.gif)
![(res2qφ = Table[D[res2/2, PDq[i], PDφ[j]], {i, 3}, {j, 3}]//TrigReduce//Simplify)//MatrixForm](HTMLFiles/index_232.gif)
![(res2φφ = Table[D[res2/2, PDφ[i], PDφ[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_233.gif)
![( {{1/8 (5 + 3 Cos[2 φ]), 3/8 Sin[2 φ], 0}, {3/8 Sin[2 φ], 1/8 (5 - 3 Cos[2 φ]), 0}, {0, 0, 1/4}} )](HTMLFiles/index_234.gif)
![( {{-3/8 Sin[2 φ] q, 3/8 (-3 + Cos[2 φ]) q, 0}, {3/8 (3 + Cos[2 φ]) q, 3/8 Sin[2 φ] q, 0}, {0, 0, 0}} )](HTMLFiles/index_235.gif)
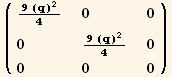
![res2qq == 1/Underscript[q, _]^2Q2§val . Q2§val//Simplify](HTMLFiles/index_237.gif)
![res2qφ == 1/4 D[Q2§val, Underscript[φ, _]] - 9/8Underscript[q, _] 2//Simplify](HTMLFiles/index_238.gif)
![res2φφ == 9/4Underscript[q, _]^22//Simplify](HTMLFiles/index_239.gif)


III. Form 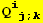
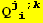
![CovariantD[Qud[i, j], k] ContravariantD[(Qud[j, i]/.l→h), k]](HTMLFiles/index_247.gif)
![%//StandardDownIndices[g]//ReleaseHoldD//EinsteinSum[] ;](HTMLFiles/index_248.gif)
![%/.CovariantD[Tensor[t__], i_] :→PartialD[labs][Tensor[t], xu[i]] ; (*the basis is orhonormal *)](HTMLFiles/index_249.gif)

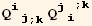
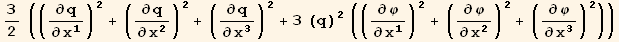

![(res3qq = Table[D[res3/2, PDq[i], PDq[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_254.gif)
![(res3qφ = Table[D[res3/2, PDq[i], PDφ[j]], {i, 3}, {j, 3}]//TrigReduce//Simplify)//MatrixForm](HTMLFiles/index_255.gif)
![(res3φφ = Table[D[res3/2, PDφ[i], PDφ[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_256.gif)
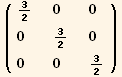
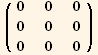
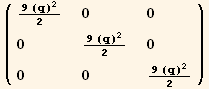
![ResultFrame[resLCI5 = CovariantD[Qud[i, j], k] ContravariantD[(Qud[j, i]/.l→h), k] == 3/2 ∇q . ∇q + 9q^2/2 ∇φ . ∇φ]](HTMLFiles/index_260.gif)
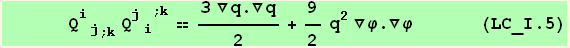
IV. Form 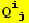
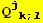

![(Qud[i, j] CovariantD[Qud[j, k], l]) (ContravariantD[(Qud[k, i]), l])](HTMLFiles/index_265.gif)
![%//StandardDownIndices[g]//ReleaseHoldD//EinsteinSum[] ;](HTMLFiles/index_266.gif)
![%/.CovariantD[Tensor[t__], i_] :→PartialD[labs][Tensor[t], xu[i]] ; (*the basis is orhonormal *)](HTMLFiles/index_267.gif)

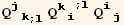
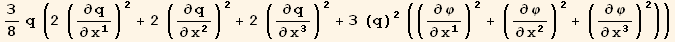

![(res4qq = Table[D[res4/2, PDq[i], PDq[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_272.gif)
![(res4qφ = Table[D[res4/2, PDq[i], PDφ[j]], {i, 3}, {j, 3}]//TrigReduce//Simplify)//MatrixForm](HTMLFiles/index_273.gif)
![(res4φφ = Table[D[res4/2, PDφ[i], PDφ[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_274.gif)
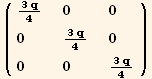
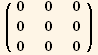
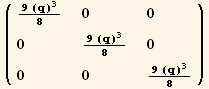
![ResultFrame[resLCI6 = (Qud[i, j] CovariantD[Qud[j, k], l]) (ContravariantD[(Qud[k, i]), l]) == 3q/4 ∇q . ∇q + 9q^3/8 ∇φ . ∇φ]](HTMLFiles/index_278.gif)
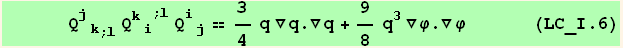
V. Form 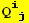
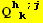

![(Qud[i, j] CovariantD[Qud[k, h], i]) (ContravariantD[(Qud[h, k]), j])](HTMLFiles/index_283.gif)
![%//StandardDownIndices[g]//ReleaseHoldD//EinsteinSum[] ;](HTMLFiles/index_284.gif)
![%/.CovariantD[Tensor[t__], i_] :→PartialD[labs][Tensor[t], xu[i]] ; (*the basis is orhonormal *)](HTMLFiles/index_285.gif)

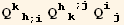
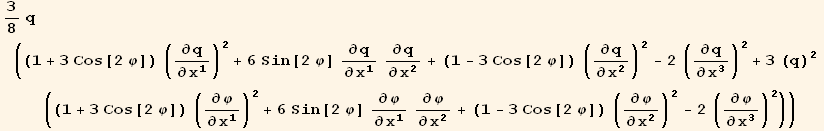

![(res5qq = Table[D[res5/2, PDq[i], PDq[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_290.gif)
![(res5qφ = Table[D[res5/2, PDq[i], PDφ[j]], {i, 3}, {j, 3}]//TrigReduce//Simplify)//MatrixForm](HTMLFiles/index_291.gif)
![(res5φφ = Table[D[res5/2, PDφ[i], PDφ[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_292.gif)
![( {{3/8 (1 + 3 Cos[2 φ]) q, 9/8 Sin[2 φ] q, 0}, {9/8 Sin[2 φ] q, 3/8 (1 - 3 Cos[2 φ]) q, 0}, {0, 0, -(3 q)/4}} )](HTMLFiles/index_293.gif)

![( {{9/8 (1 + 3 Cos[2 φ]) (q)^3, 27/8 Sin[2 φ] (q)^3, 0}, {27/8 Sin[2 φ] (q)^3, 9/8 (1 - 3 Cos[2 φ]) (q)^3, 0}, {0, 0, -(9 (q)^3)/4}} )](HTMLFiles/index_295.gif)
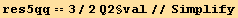
![res5φφ == 9Underscript[q, _]^2/2 Q2§val//Simplify](HTMLFiles/index_297.gif)
![ResultFrame[resLCI7 = (Qud[i, j] CovariantD[Qud[k, h], i]) (ContravariantD[(Qud[h, k]), j]) == 3/2 ∇q . Q . ∇q + 9q^2/2 ∇φ . Q . ∇φ]](HTMLFiles/index_300.gif)
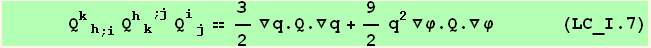
VI. Form 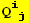
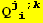
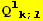
![(Qud[i, j] CovariantD[Qud[l, k], l]) (ContravariantD[(Qud[j, i]), k])](HTMLFiles/index_305.gif)
![%//StandardDownIndices[g]//ReleaseHoldD//EinsteinSum[] ;](HTMLFiles/index_306.gif)
![%/.CovariantD[Tensor[t__], i_] :→PartialD[labs][Tensor[t], xu[i]] ; (*the basis is orhonormal *)](HTMLFiles/index_307.gif)

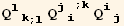
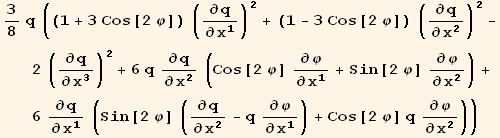

![(res6qq = Table[D[res6/2, PDq[i], PDq[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_312.gif)
![(res6qφ = Table[D[res6/2, PDq[i], PDφ[j]], {i, 3}, {j, 3}]//TrigReduce//Simplify)//MatrixForm](HTMLFiles/index_313.gif)
![(res6φφ = Table[D[res6/2, PDφ[i], PDφ[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_314.gif)
![( {{3/8 (1 + 3 Cos[2 φ]) q, 9/8 Sin[2 φ] q, 0}, {9/8 Sin[2 φ] q, 3/8 (1 - 3 Cos[2 φ]) q, 0}, {0, 0, -(3 q)/4}} )](HTMLFiles/index_315.gif)
![( {{-9/8 Sin[2 φ] (q)^2, 9/8 Cos[2 φ] (q)^2, 0}, {9/8 Cos[2 φ] (q)^2, 9/8 Sin[2 φ] (q)^2, 0}, {0, 0, 0}} )](HTMLFiles/index_316.gif)
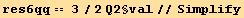
![res6qφ == 3/4 Underscript[q, _] D[Q2§val, Underscript[φ, _]]//Simplify](HTMLFiles/index_319.gif)
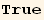
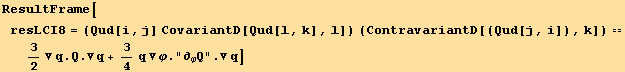
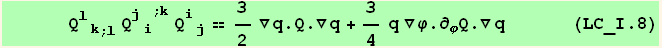
VII. Form 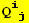
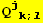

![(Qud[i, j] CovariantD[Qud[j, k], l]) (ContravariantD[(Qud[l, i]), k])](HTMLFiles/index_327.gif)
![%//StandardDownIndices[g]//ReleaseHoldD//EinsteinSum[] ;](HTMLFiles/index_328.gif)
![%/.CovariantD[Tensor[t__], i_] :→PartialD[labs][Tensor[t], xu[i]] ; (*the basis is orhonormal *)](HTMLFiles/index_329.gif)

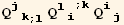
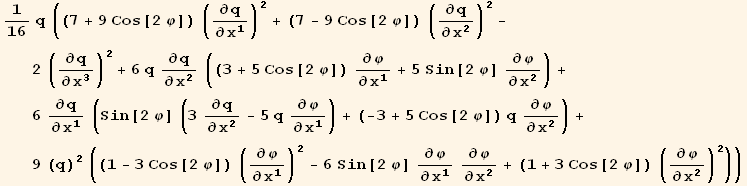

![(res7qq = Table[D[res7/2, PDq[i], PDq[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_334.gif)
![(res7qφ = Table[D[res7/2, PDq[i], PDφ[j]], {i, 3}, {j, 3}]//TrigReduce//Simplify)//MatrixForm](HTMLFiles/index_335.gif)
![(res7φφ = Table[D[res7/2, PDφ[i], PDφ[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_336.gif)
![( {{1/16 (7 + 9 Cos[2 φ]) q, 9/16 Sin[2 φ] q, 0}, {9/16 Sin[2 φ] q, 1/16 (7 - 9 Cos[2 φ]) q, 0}, {0, 0, -q/8}} )](HTMLFiles/index_337.gif)
![( {{-15/16 Sin[2 φ] (q)^2, 3/16 (-3 + 5 Cos[2 φ]) (q)^2, 0}, {3/16 (3 + 5 Cos[2 φ]) (q)^2, 15/16 Sin[2 φ] (q)^2, 0}, {0, 0, 0}} )](HTMLFiles/index_338.gif)
![( {{9/16 (1 - 3 Cos[2 φ]) (q)^3, -27/16 Sin[2 φ] (q)^3, 0}, {-27/16 Sin[2 φ] (q)^3, 9/16 (1 + 3 Cos[2 φ]) (q)^3, 0}, {0, 0, 0}} )](HTMLFiles/index_339.gif)
![res7qq == 1/Underscript[q, _]^2Q2§val . Q2§val . Q2§val//Simplify](HTMLFiles/index_340.gif)
![res7qφ == 5/8 Underscript[q, _] D[(Q2§val), Underscript[φ, _]] - 9/16Underscript[q, _]^22//Simplify](HTMLFiles/index_341.gif)
![res7φφ == -9/2 Underscript[q, _] (Q2§val . Q2§val) + 9/8Underscript[q, _]^3 + 9/4Underscript[q, _]^32//Simplify](HTMLFiles/index_342.gif)

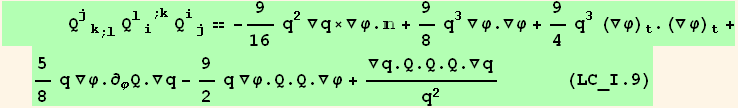
![(Qud[i, j] CovariantD[Qud[j, k], l]) (ContravariantD[(Qud[l, i]), k]) == (Qud[i, j] CovariantD[Qud[l, k], l]) (ContravariantD[(Qud[k, i]), j])](HTMLFiles/index_348.gif)

VIII. Form 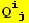
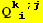
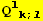
![(Qud[i, j] CovariantD[Qud[l, k], l]) (ContravariantD[(Qud[k, i]), j])](HTMLFiles/index_353.gif)
![%//StandardDownIndices[g]//ReleaseHoldD//EinsteinSum[] ;](HTMLFiles/index_354.gif)
![%/.CovariantD[Tensor[t__], i_] :→PartialD[labs][Tensor[t], xu[i]] ; (*the basis is orhonormal *)](HTMLFiles/index_355.gif)

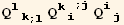
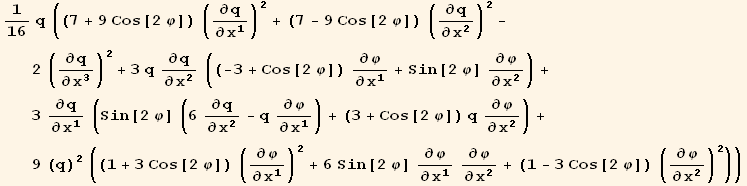

![(res8qq = Table[D[res8/2, PDq[i], PDq[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_360.gif)
![(res8qφ = Table[D[res8/2, PDq[i], PDφ[j]], {i, 3}, {j, 3}]//TrigReduce//Simplify)//MatrixForm](HTMLFiles/index_361.gif)
![(res8φφ = Table[D[res8/2, PDφ[i], PDφ[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_362.gif)
![( {{1/16 (7 + 9 Cos[2 φ]) q, 9/16 Sin[2 φ] q, 0}, {9/16 Sin[2 φ] q, 1/16 (7 - 9 Cos[2 φ]) q, 0}, {0, 0, -q/8}} )](HTMLFiles/index_363.gif)
![( {{-3/32 Sin[2 φ] (q)^2, 3/32 (3 + Cos[2 φ]) (q)^2, 0}, {3/32 (-3 + Cos[2 φ]) (q)^2, 3/32 Sin[2 φ] (q)^2, 0}, {0, 0, 0}} )](HTMLFiles/index_364.gif)
![( {{9/16 (1 + 3 Cos[2 φ]) (q)^3, 27/16 Sin[2 φ] (q)^3, 0}, {27/16 Sin[2 φ] (q)^3, 9/16 (1 - 3 Cos[2 φ]) (q)^3, 0}, {0, 0, 0}} )](HTMLFiles/index_365.gif)
![res8qq == 1/Underscript[q, _]^2Q2§val . Q2§val . Q2§val//Simplify](HTMLFiles/index_366.gif)
![res8qφ == 1/16 Underscript[q, _] D[(Q2§val), Underscript[φ, _]] + 9/32Underscript[q, _]^22//Simplify](HTMLFiles/index_367.gif)
![res8φφ == 9/2 Underscript[q, _] (Q2§val . Q2§val) - 9/8Underscript[q, _]^3 - 9/8Underscript[q, _]^32//Simplify](HTMLFiles/index_368.gif)

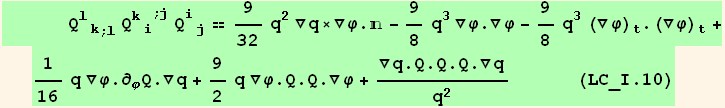
IX. Form 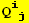
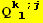
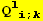
![(Qud[i, j] CovariantD[Qud[l, i], k]) (ContravariantD[(Qud[k, l]), j])](HTMLFiles/index_377.gif)
![%//StandardDownIndices[g]//ReleaseHoldD//EinsteinSum[] ;](HTMLFiles/index_378.gif)
![%/.CovariantD[Tensor[t__], i_] :→PartialD[labs][Tensor[t], xu[i]] ; (*the basis is orhonormal *)](HTMLFiles/index_379.gif)

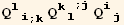
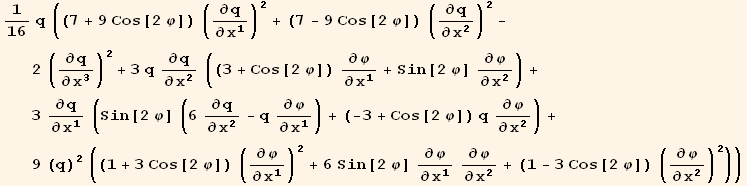

![(res9qq = Table[D[res9/2, PDq[i], PDq[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_384.gif)
![(res9qφ = Table[D[res9/2, PDq[i], PDφ[j]], {i, 3}, {j, 3}]//TrigReduce//Simplify)//MatrixForm](HTMLFiles/index_385.gif)
![(res9φφ = Table[D[res9/2, PDφ[i], PDφ[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_386.gif)
![( {{1/16 (7 + 9 Cos[2 φ]) q, 9/16 Sin[2 φ] q, 0}, {9/16 Sin[2 φ] q, 1/16 (7 - 9 Cos[2 φ]) q, 0}, {0, 0, -q/8}} )](HTMLFiles/index_387.gif)
![( {{-3/32 Sin[2 φ] (q)^2, 3/32 (-3 + Cos[2 φ]) (q)^2, 0}, {3/32 (3 + Cos[2 φ]) (q)^2, 3/32 Sin[2 φ] (q)^2, 0}, {0, 0, 0}} )](HTMLFiles/index_388.gif)
![( {{9/16 (1 + 3 Cos[2 φ]) (q)^3, 27/16 Sin[2 φ] (q)^3, 0}, {27/16 Sin[2 φ] (q)^3, 9/16 (1 - 3 Cos[2 φ]) (q)^3, 0}, {0, 0, 0}} )](HTMLFiles/index_389.gif)
![res9qq == 1/Underscript[q, _]^2 (Q2§val . Q2§val . Q2§val//FullSimplify)](HTMLFiles/index_390.gif)
![res9qφ == Underscript[q, _]/16D[Q2§val, Underscript[φ, _]] - 9/32Underscript[q, _]^22//Simplify](HTMLFiles/index_391.gif)
![res9φφ == 9/2 Underscript[q, _] Q2§val . Q2§val - 9/8Underscript[q, _]^3 - 9/8Underscript[q, _]^32//FullSimplify](HTMLFiles/index_392.gif)

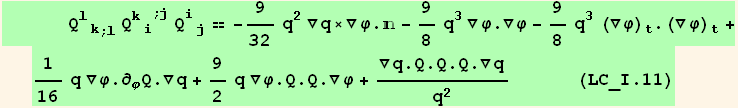
X. Form 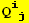
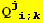

![(Qud[i, j] CovariantD[Qud[j, i], k]) (ContravariantD[(Qud[k, l]), l])](HTMLFiles/index_401.gif)
![%//StandardDownIndices[g]//ReleaseHoldD//EinsteinSum[] ;](HTMLFiles/index_402.gif)
![%/.CovariantD[Tensor[t__], i_] :→PartialD[labs][Tensor[t], xu[i]] ; (*the basis is orhonormal *)](HTMLFiles/index_403.gif)
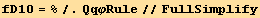
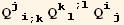
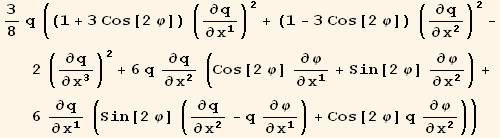

![(res10qq = Table[D[res10/2, PDq[i], PDq[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_408.gif)
![(res10qφ = Table[D[res10/2, PDq[i], PDφ[j]], {i, 3}, {j, 3}]//TrigReduce//Simplify)//MatrixForm](HTMLFiles/index_409.gif)
![(res10φφ = Table[D[res10/2, PDφ[i], PDφ[j]], {i, 3}, {j, 3}]//Simplify)//MatrixForm](HTMLFiles/index_410.gif)
![( {{3/8 (1 + 3 Cos[2 φ]) q, 9/8 Sin[2 φ] q, 0}, {9/8 Sin[2 φ] q, 3/8 (1 - 3 Cos[2 φ]) q, 0}, {0, 0, -(3 q)/4}} )](HTMLFiles/index_411.gif)
![( {{-9/8 Sin[2 φ] (q)^2, 9/8 Cos[2 φ] (q)^2, 0}, {9/8 Cos[2 φ] (q)^2, 9/8 Sin[2 φ] (q)^2, 0}, {0, 0, 0}} )](HTMLFiles/index_412.gif)
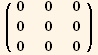
![res10qq == 2/ Underscript[q, _]^2 Q2§val . Q2§val . Q2§val - 1/2 Underscript[q, _] //FullSimplify](HTMLFiles/index_414.gif)
![res10qφ == 3 Underscript[q, _]/4D[Q2§val, Underscript[φ, _]]//Simplify](HTMLFiles/index_415.gif)
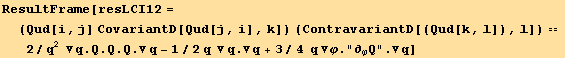

XI. Combinations 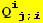
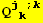 and
and 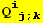
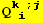
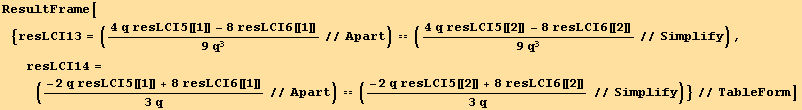

Simplifications
Some of the above expression may be simplified. This leads to a simplification rule (Simplifrule) :
![Q2§val . Q2§val == Underscript[q, _]/2 Q2§val + Underscript[q, _]^2/2 //Simplify](HTMLFiles/index_428.gif)
![Q2§val . Q2§val . Q2§val == 3/4 Underscript[q, _]^2Q2§val + Underscript[q, _]^3/4 //Simplify](HTMLFiles/index_429.gif)
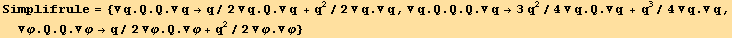
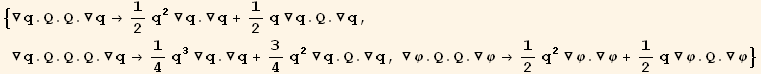
C. RESUME
We summarize below all the results :

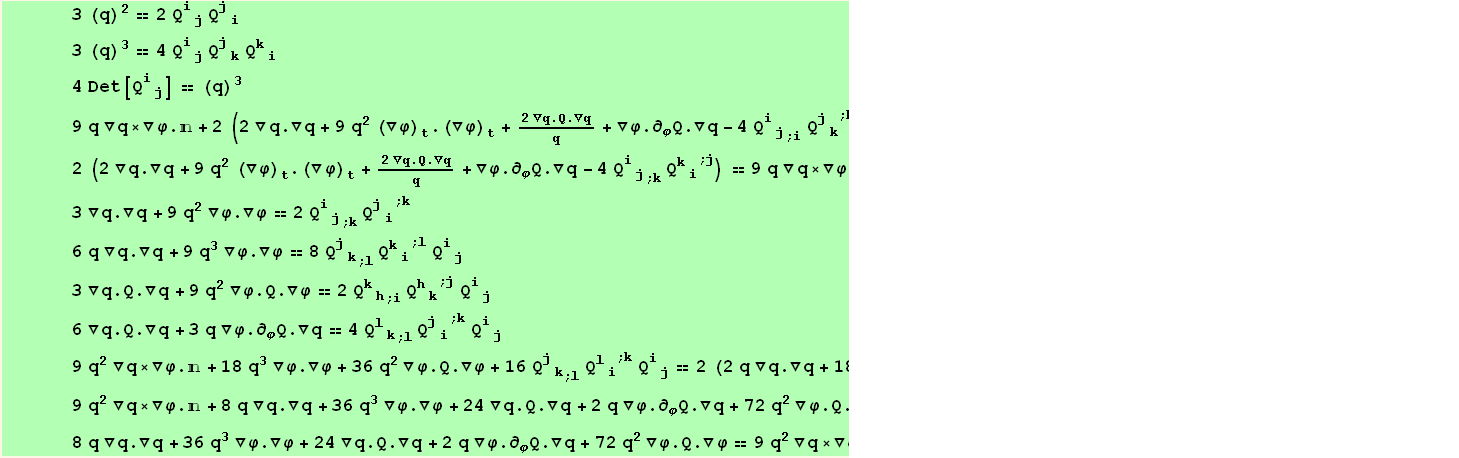
Another question is : what are the expressions involving ∇q and ∇φ as functions of the 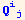 and its covariant derivatives.
and its covariant derivatives.
To do this we have to invert the above expressions.
Inversion
We first introduce shortened notations for the various terms, and find how some of them are related :
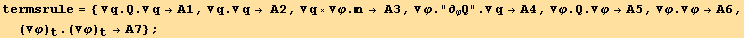
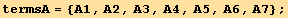
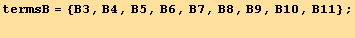

![Eliminate[(M . termsA == termsB), termsA]](HTMLFiles/index_441.gif)
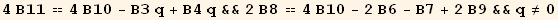

we check the validity of these relations :

![zero[a_, b_] = a (4B11 - (4B10 - B3 q + B4 q)) + b (-8q (2B8 - (4 * B10 - 2 * B6 - B7 + 2 * B9))) ;](HTMLFiles/index_445.gif)
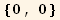
... and obtain the expected inverse relation :
![AtoBrule = Solve[(M . termsA == termsB/.{B11→ (4B10 - B3 q + B4 q)/4, B8→ (4 * B10 - 2 * B6 - B7 + 2 * B9)/2}), termsA][[1]]](HTMLFiles/index_447.gif)
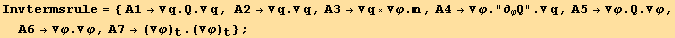
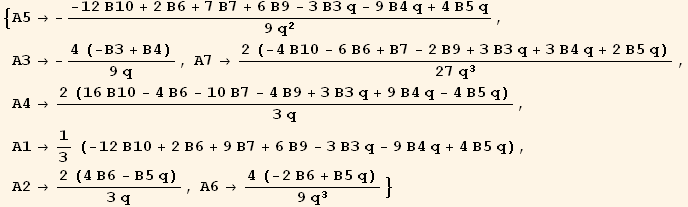
D. RESUME (inversion)
![QToBrule = Table[Rule[#2, #1] & @@ (BToQrule[[i$]]), {i$, Length[BToQrule]}]/.{i→i_, j→j_, k→k_, l→l_}](HTMLFiles/index_450.gif)
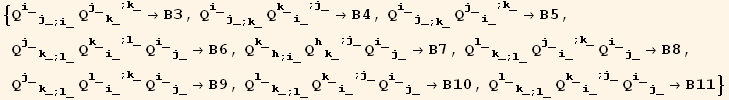
![(resLCI12/.Simplifrule//Simplify)[[2]] == (resLCI8/.Simplifrule//Simplify)[[2]]](HTMLFiles/index_452.gif)
![ResultFrame[RES = {resLCI12[[1]] == resLCI8[[1]], Collect[4B11 - (4B10 - B3 q + B4 q), q, Factor] == 0, 2B8 - (4B10 - 2B6 - B7 + 2B9) == 0}/.BToQrule//TableForm]](HTMLFiles/index_453.gif)
![Print["with again a check of the relations involving B :"]](HTMLFiles/index_454.gif)
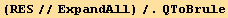
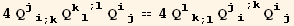
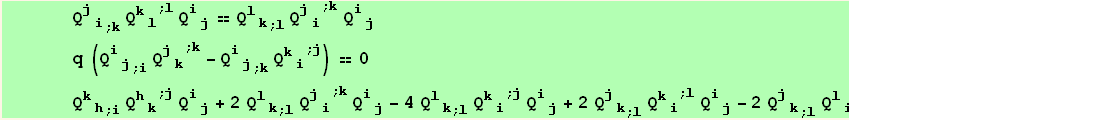
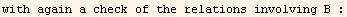
 |
| B3 q-B4 q==0 |
| -4 B10+2 B6+B7+2 B8-2 B9==0 |
All the results are summarized here :

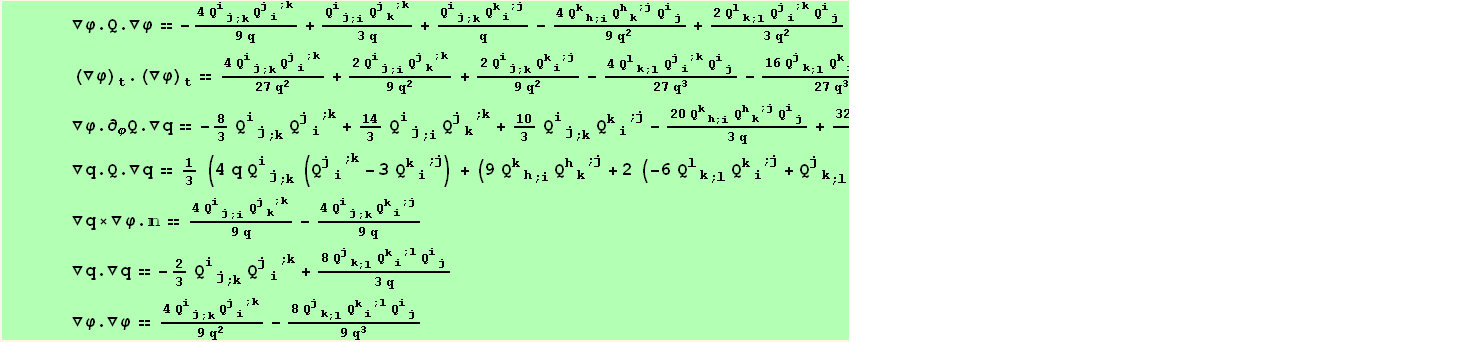
A more general approach
Free Energy: Homogeneous form
The Landau free energy of a nematic-isotropic system may be written up to fourth order in Q :
![equfw = fw[q] == A/2δ[q] + B/3Δ[q] + C/4δ[q]^2](HTMLFiles/index_462.gif)
![rulδ = δ[q] →Tensor[Qud[i, j] Qud[j, i]]](HTMLFiles/index_463.gif)
![rulΔ = Δ[q] →Tensor[Qud[i, j] Qud[j, k] Qud[k, i]]](HTMLFiles/index_464.gif)
![ResultFrame[equfw/.{rulδ, rulΔ}]](HTMLFiles/index_465.gif)
![fw[q] == 1/2 A δ[q] + 1/4 C δ[q]^2 + 1/3 B Δ[q]](HTMLFiles/index_466.gif)
![δ[q] →Q_ (ij)^(ij) Q_ (ji)^(ji)](HTMLFiles/index_467.gif)
![Δ[q] →Q_ (ij)^(ij) Q_ (jk)^(jk) Q_ (ki)^(ki)](HTMLFiles/index_468.gif)

these rotational invariants only depend on q :
![Q$ud[i_, j_] := Q§ud[i, j]/.tu[k_] td[k_] →3q/2<br />](HTMLFiles/index_470.gif)
![equδ = δ[q] == (Q$ud[i, j] Q$ud[j, i]//Expand//MetricSimplify[g])//.tu[k_] td[k_] →3q/2/.gud[i_, i_] →NDim](HTMLFiles/index_471.gif)
![equΔ = Δ[q] == (Q$ud[i, j] Q$ud[j, k] Q$ud[k, i]//Expand//MetricSimplify[g])//.tu[k_] td[k_] →3q/2/.gud[i_, i_] →NDim](HTMLFiles/index_472.gif)
![δ[q] == (3 q^2)/2](HTMLFiles/index_473.gif)
![Δ[q] == (3 q^3)/4](HTMLFiles/index_474.gif)
and the corresponding free energy is,
![equf = equfw/.{equδ[[1]] →equδ[[2]], equΔ[[1]] →equΔ[[2]]}](HTMLFiles/index_475.gif)
![fw[q] == (3 A q^2)/4 + (B q^3)/4 + (9 C q^4)/16](HTMLFiles/index_476.gif)
fw will be chosen in the form: fq = 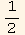
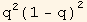 . This fixes A,B, and C (rulABC):
. This fixes A,B, and C (rulABC):
![equfq = fq[q] == 1/2 q^2 (1 - q)^2](HTMLFiles/index_479.gif)
![Collect[equfq[[2]] - equf[[2]], {q}]](HTMLFiles/index_480.gif)
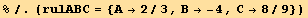
![fq[q] == 1/2 (1 - q)^2 q^2](HTMLFiles/index_482.gif)
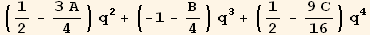

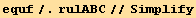
![(-1 + q)^2 q^2 == 2 fw[q]](HTMLFiles/index_486.gif)
Now the free energy has the general expression :
![ResultFrame[equfw/.rulABC]](HTMLFiles/index_487.gif)
![fw[q] == δ[q]/3 + (2 δ[q]^2)/9 - (4 Δ[q])/3 (LC_I.18)](HTMLFiles/index_488.gif)
List of invariants built with t, div[t], curl[t], grad[ ], grad[t], Δ[t]
], grad[t], Δ[t]
We can now generate the invariants built with t.
We use the operators defined in TContinuumMechanics (TDiv,TGrad,TCurl,TLaplacian).
![2 2[i_] = == Tensor[t, {i}, {Void}] * Tensor[t, {Void}, {i}] <br />](HTMLFiles/index_490.gif)
![div[i_] = "div[]" == TDiv[, g, i][ ] <br />](HTMLFiles/index_491.gif)
![2 div2[i_, j_] = div[ ] == TDiv[, g, i][ ] TDiv[, g, j][ ]](HTMLFiles/index_492.gif)
![gradgrad[p_, q_] = "grad[].grad[]" == (TGrad[, p][tu[q]] . TGrad[, r][td[q]]//EvaluateDotProducts[, g]//MetricSimplifyD[g])](HTMLFiles/index_493.gif)
![curl[i_, j_, k_] = "curl[]" == TCurl[, g, {i, j, k}, e][] ;](HTMLFiles/index_494.gif)

![res1 = (/.k→p) . TGrad[, i][tu[q] td[q]]//EvaluateDotProducts[, g] ;](HTMLFiles/index_496.gif)
![2 grad[p_, q_] = .grad[ ]/2 == (res1[[1]] + (res1[[2]]//UpDownSwapD[q]))/2/.i→p](HTMLFiles/index_497.gif)
![curl = ".curl[]" == . TCurl[, g, {p, q, r}, e][]//EvaluateDotProducts[, g] ;](HTMLFiles/index_498.gif)
![res2 = curl[[2]] (curl[[2]]/.{p→i, q→j, k→h})//FullLeviCivitaExpand[e, g]//MetricSimplifyD[g] ;](HTMLFiles/index_499.gif)

![res = (/.k→h) ×curl[i, j, k][[2]]//EvaluateCrossProducts[, e, g, m] ;](HTMLFiles/index_501.gif)
![res3 = (res . (res/.{i→p, j→q, m→r})//EvaluateDotProducts[, g]//MetricSimplifyD[g]) ;](HTMLFiles/index_502.gif)
![res4 = (TDiv[, g, h][res]//MetricSimplifyD[g]) ;](HTMLFiles/index_504.gif)
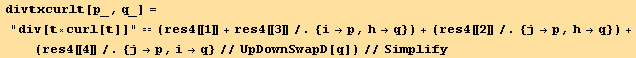
![2 2 2curl2[p_, q_, r_] = (curl[]) == tu[r] td[r] curl2[p, q][[2]]](HTMLFiles/index_506.gif)
![res5 = (TGrad[, i][tu[p] td[p]] . TGrad[, q][tu[r] td[r]]//EvaluateDotProducts[, g]//MetricSimplifyD[g])/.i→q ;](HTMLFiles/index_507.gif)

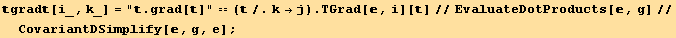
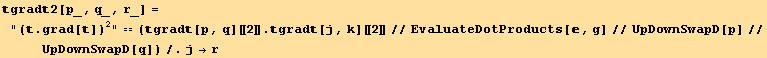
![divdiv[p_, q_] = "div[div]" == TDiv[, g, q][ TDiv[, g, p][ ]]](HTMLFiles/index_511.gif)
![res6 = TLaplacian[, g, q, r][2[p][[2]]]//MetricSimplifyD[g] ;](HTMLFiles/index_512.gif)

![res7 = TLaplacian[, g, q, p][]//MetricSimplifyD[g] ;](HTMLFiles/index_514.gif)
![lapl[p_, q_] = "Δ[]" == (/.k→r) . res7//EvaluateDotProducts[, g]//UpDownSwapD[k, p]](HTMLFiles/index_515.gif)
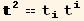
![div[] == t_i^i_ (; i)](HTMLFiles/index_517.gif)
![2 div[ ] == t_i^i_ (; i) t_j^j_ (; j)](HTMLFiles/index_518.gif)
![grad[].grad[] == t_q^q_ (; p) t_q^q^(; p)](HTMLFiles/index_519.gif)
![2 curl[ ] == -t_p^p_ (; q) t_q^q_ (; p) + t_q^q_ (; p) t_q^q^(; p)](HTMLFiles/index_520.gif)
![2 .grad[ ]/2 == t_q^q_ (; p) t_q^q t_p^p](HTMLFiles/index_521.gif)
![2 (.curl[]) == -(t_p^p_ (; q) - t_q^q^(; p)) ((-t_q^q_ (; r) + t_r^r^(; q)) t_p^p t_r^r + t_q^q_ (; p) t_r^r t_r^r)](HTMLFiles/index_522.gif)
![2 (×curl[]) == -(t_p^p_ (; q) - t_q^q^(; p)) (t_q^q_ (; r) - t_r^r^(; q)) t_p^p t_r^r](HTMLFiles/index_523.gif)
![div[×curl[]] == t_p^p_ (; q) (-t_q^q_ (; p) + t_p^p^(; q)) + ((t_p^p^(; q)) _ (; q) - t_q^q_ (; pq)) t_p^p](HTMLFiles/index_524.gif)
![2 2 (curl[]) == (-t_p^p_ (; q) t_q^q_ (; p) + t_q^q_ (; p) t_q^q^(; p)) t_r^r t_r^r](HTMLFiles/index_525.gif)
![2 2 grad[ ] /4 == t_p^p_ (; q) t_r^r^(; q) t_p^p t_r^r](HTMLFiles/index_526.gif)
![2 (.grad[]) == t_q^q_ (; r) t_q^q^(; p) t_p^p t_r^r](HTMLFiles/index_527.gif)
![div[div] == t_p^p_ (; p) t_q^q_ (; q) + t_p^p_ (; pq) t_q^q](HTMLFiles/index_528.gif)
![2 Δ[ ] == 2 t_p^p_ (; q) t_p^p^(; q) + 2 (t_p^p^(; r)) _ (; r) t_p^p](HTMLFiles/index_529.gif)
![Δ[] == (t_p^p^(; q)) _ (; q) t_p^p](HTMLFiles/index_530.gif)
List of terms of order one and three in t, with zero, and first order derivatives,
![listOdd = {div[i][[2]], grad[i, j][[2]]}](HTMLFiles/index_531.gif)
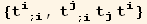
List of terms of order two in t, with zero, first and second order derivatives,
![listSq1 = {2[i][[2]], div[i][[2]] (div[j][[2]]), -curl2[i, j][[2, 1]], curl2[i, j][[2, 2]]}](HTMLFiles/index_533.gif)
![listSq2 = {tu[i] CovariantD[tu[j], {i, j}], tu[i] CovariantD[ContravariantD[td[i], j], j]}](HTMLFiles/index_534.gif)
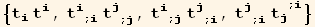
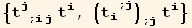
![listSq = Union[listSq1, listSq2]](HTMLFiles/index_537.gif)
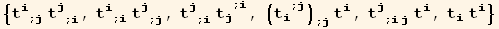
List of terms of order four in t, with zero and first order derivatives,
![listQa = Table[tu[p] td[i] CovariantD[tu[q], j] CovariantD[tu[r], k]/.Apply[Rule, Transpose[{{p, q, r}, Permutations[{i, j, k}][[n]]}], {1}], {n, 6}]//Sort](HTMLFiles/index_539.gif)

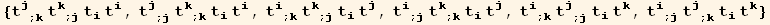
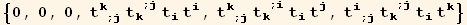
In listQb, the factors 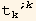 ≡
≡ 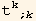 are already in listQa, so we have cancelled the corresponding terms
are already in listQa, so we have cancelled the corresponding terms
In addition, the following terms are duplicated in the list listQa :
![{listQa[[5]], listQa[[6]]}/.{k→j, j→k}](HTMLFiles/index_545.gif)
![% == {listQa[[4]], listQa[[3]]}](HTMLFiles/index_546.gif)
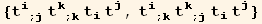
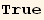
So in the general case, there exists seven invariants of this type :
![res = Union[Take[listQa, 4], Take[listQb, -3]] ;](HTMLFiles/index_549.gif)
![listQu = (tu[i] td[i] Coefficient[res, tu[i] td[i]] + tu[j] td[i] Coefficient[res, tu[j] td[i]] + tu[j] td[i] (Coefficient[res, tu[k] td[i]]/.{k→j, j→k}))//Sort](HTMLFiles/index_550.gif)
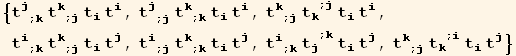
Notations for the invariants : Sq for order two, Qu for order four.

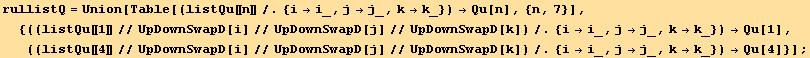
![rullistOd = Table[(listOdd[[n]]/.{i→i_, j→j_, k→k_}) →Od[n], {n, 2}] ;](HTMLFiles/index_554.gif)
![ResultFrame[rullist = {2[i_][[2]] →2[i][[1]], rullistSq, rullistQ, rullistOd}//Flatten]](HTMLFiles/index_555.gif)
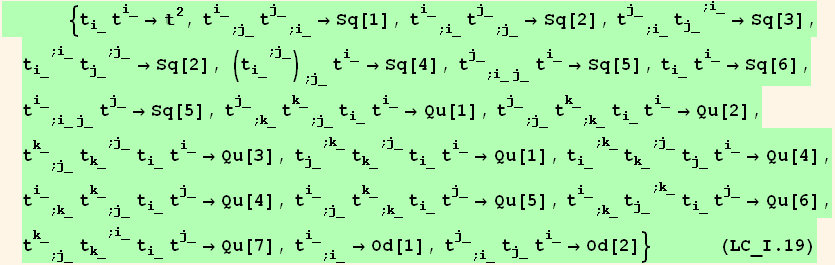
Correspondence between the list of invariant and the Divergence, Curl, Laplacian... forms,
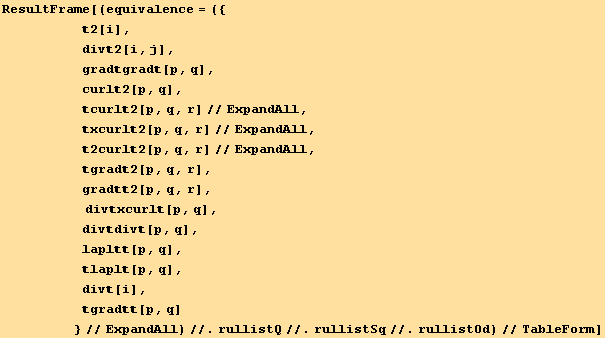

while the inverse relation is,
![Print["We have the following relations between the functions :"]](HTMLFiles/index_559.gif)

![relS1 = Solve[relationsS[[1]]/."div[×curl[]]"→X, X][[1, 1]]/.X→"div[×curl[]]"](HTMLFiles/index_561.gif)
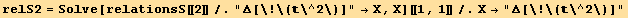

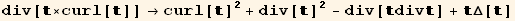
![2 Δ[ ] →2 (grad[].grad[] + Δ[])](HTMLFiles/index_565.gif)
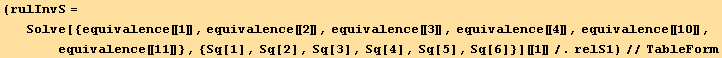
![2 Sq[1] → -curl[ ] + grad[].grad[]](HTMLFiles/index_567.gif) |
![2 Sq[2] →div[ ]](HTMLFiles/index_568.gif) |
| Sq[3]→grad[t].grad[t] |
| Sq[4]→tΔ[t] |
![2 Sq[5] → -div[ ] + div[div]](HTMLFiles/index_569.gif) |
![2 Sq[6] → ](HTMLFiles/index_570.gif) |
![Print["We have the third relation between the functions :"]](HTMLFiles/index_571.gif)
![relationsQ = Eliminate[{equivalence[[5]], equivalence[[6]], equivalence[[7]], equivalence[[8]], equivalence[[9]]}, {Qu[1], Qu[2], Qu[3], Qu[4], Qu[5], Qu[6], Qu[7]}] ;](HTMLFiles/index_572.gif)
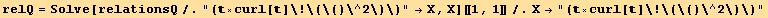

![2 2 2 2 (×curl[]) → (curl[]) - (.curl[])](HTMLFiles/index_575.gif)
![(rulInvOd = Solve[{equivalence[[14]], equivalence[[15]]}, {Od[1], Od[2]}][[1]])//TableForm](HTMLFiles/index_576.gif)
| Od[1]→div[t] |
![2 Od[2] →.grad[ ]/2](HTMLFiles/index_577.gif) |
![resQu67 = Solve[{equivalence[[8]], equivalence[[9]]}, {Qu[6], Qu[7]}][[1]] ;](HTMLFiles/index_578.gif)
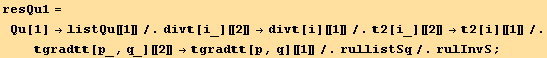
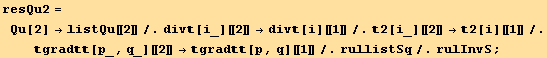
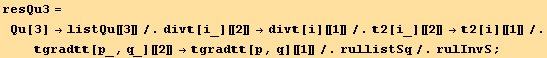
![resQu4 = Qu[4] → ( Qu[4]/.Solve[equivalence[[6]]/.resQu67, Qu[4]][[1]]) ;](HTMLFiles/index_582.gif)
![resQu5 = Qu[5] →listQu[[5]]/.div[i_][[2]] →div[i][[1]]/.grad[p_, q_][[2]] →grad[p, q][[1]] ;](HTMLFiles/index_583.gif)


There exists the following three identities :
![ResultFrame[(identities = {relationsS[[1]], relationsS[[2]], relationsQ})//TableForm]](HTMLFiles/index_593.gif)
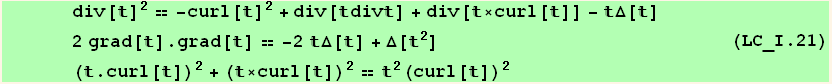
What is the meaning of the term "grad[t].grad[t]" ?
Now we showx that gradtgradt is the sum of a divergence div[...] plus curl[t\!\(\(]\^2\)\)+div[t\!\(\(]\^2\)\):
We start from the two last identities (valid for arbitrary t) :
![identities[[1]]](HTMLFiles/index_595.gif)
![identities[[2]]](HTMLFiles/index_596.gif)
![2 2 div[ ] == -curl[ ] + div[div] + div[×curl[]] - Δ[]](HTMLFiles/index_597.gif)
![2 2 grad[].grad[] == -2 Δ[] + Δ[ ]](HTMLFiles/index_598.gif)
and eliminate tΔ[t] :
![Eliminate[{identities[[1]], identities[[2]]}/.(-identities[[1, 2, 4]]) →x, x] ;](HTMLFiles/index_599.gif)
![identities[[2, 1]]/2 == ( x/.Solve[%/.identities[[2, 1]]/2→x, x][[1]]//Simplify)](HTMLFiles/index_600.gif)
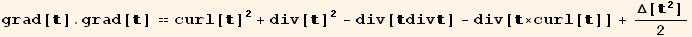
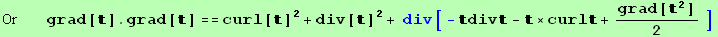

Now the expression 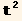 grad[t].grad[t] can be rewritten, using,
grad[t].grad[t] can be rewritten, using,

![TDiv[, g, j][ 2[i][[2]] Tensor[u, {k}, {Void}] * Tensor[, {Void}, {k}] ]//Expand ;](HTMLFiles/index_606.gif)
![2 div[ ] == %//.rul1](HTMLFiles/index_607.gif)
![2 2 2 div[ ] == grad[ ]. + div[] ](HTMLFiles/index_608.gif)
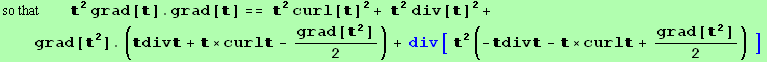
Explicit form of  K
K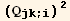 in the case
in the case 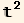 arbitrary)
arbitrary)
![(CovariantD[Q§ud[i, j], k]//CovariantDSimplify[, g, e]) (ContravariantD[(Q§ud[j, i]/.l→h), k]//CovariantDSimplify[, g, e]) ;](HTMLFiles/index_613.gif)
![res = (%//Expand//MetricSimplify[g])/.{gud[i_, i_] →NDim, gdu[i_, i_] →NDim}//Expand//TensorSimplify](HTMLFiles/index_614.gif)
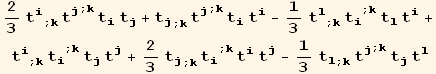

![2 (2 Qu[6])/3 + 2 Sq[3]](HTMLFiles/index_618.gif)
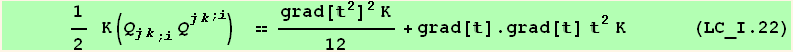
![ClearTensorShortcuts[{{, J, J1, J2, , t}, 1}, {{g, Q, Q§, Β}, 2}, {{}, 3}, {{}, 4}] ;](HTMLFiles/index_620.gif)
![( {{J_X^X}, {J_Y^Y}, {J_Z^Z}} ) == ( {{Cos[φ] Sin[θ]}, {Sin[θ] Sin[φ]}, {Cos[θ]}} )](HTMLFiles/index_37.gif)
![H12 := 3K J1u[i] J2u[j] (Coefficient[H12§/(3K)//EvaluateDotProducts[, g, False], J1u[i] J2u[j]]//MetricSimplify[g])](HTMLFiles/index_69.gif)
![( {{-1/3 Abs[t]^2 + t_1^1 t_1^1, t_2^2 t_1^1, t_3^3 t_1^1}, {t_1^1 t_2^2, -1/3 Abs[t]^2 + t_2^2 t_2^2, t_3^3 t_2^2}, {t_1^1 t_3^3, t_2^2 t_3^3, -1/3 Abs[t]^2 + t_3^3 t_3^3}} )](HTMLFiles/index_78.gif)
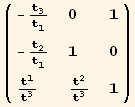
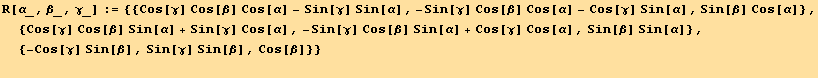
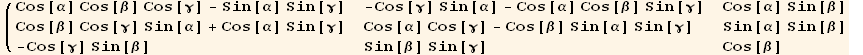
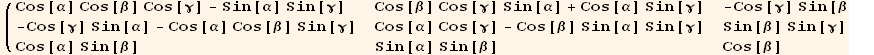
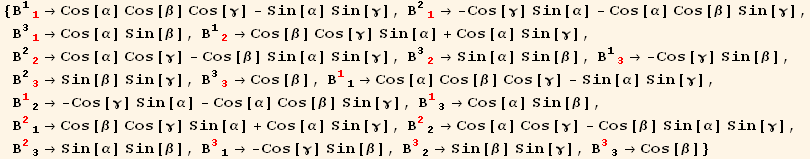


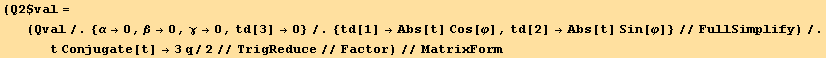
![( {{1/4 q (1 + 3 Cos[2 φ]), 3/4 q Sin[2 φ], 0}, {3/4 q Sin[2 φ], -1/4 q (-1 + 3 Cos[2 φ]), 0}, {0, 0, -q/2}} )](HTMLFiles/index_148.gif)
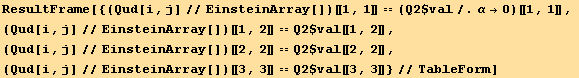
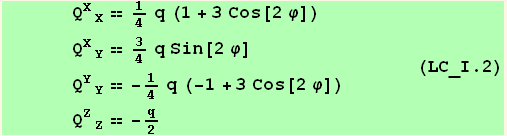


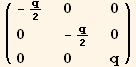
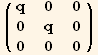
![Q_ (ij)^(ij) Q_ (jk)^(jk) == ( {{1/8 (5 + 3 Cos[2 φ]) (q)^2, 3/8 Sin[2 φ] (q)^2, 0}, {3/8 Sin[2 φ] (q)^2, 1/8 (5 - 3 Cos[2 φ]) (q)^2, 0}, {0, 0, (q)^2/4}} )](HTMLFiles/index_192.gif)
![Q_ (ij)^(ij) Q_ (jk)^(jk) Q_ (kl)^(kl) == ( {{1/16 (7 + 9 Cos[2 φ]) (q)^3, 9/16 Sin[2 φ] (q)^3, 0}, {9/16 Sin[2 φ] (q)^3, 1/16 (7 - 9 Cos[2 φ]) (q)^3, 0}, {0, 0, -(q)^3/8}} )](HTMLFiles/index_193.gif)
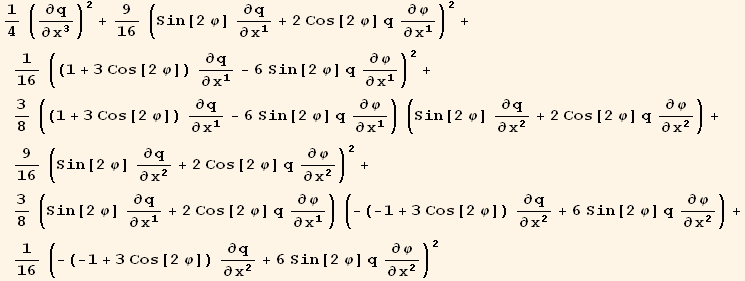

![( {{1/8 (5 + 3 Cos[2 φ]), 3/8 Sin[2 φ], 0}, {3/8 Sin[2 φ], 1/8 (5 - 3 Cos[2 φ]), 0}, {0, 0, 1/4}} )](HTMLFiles/index_208.gif)
![( {{-3/8 Sin[2 φ] q, 3/8 (3 + Cos[2 φ]) q, 0}, {3/8 (-3 + Cos[2 φ]) q, 3/8 Sin[2 φ] q, 0}, {0, 0, 0}} )](HTMLFiles/index_209.gif)



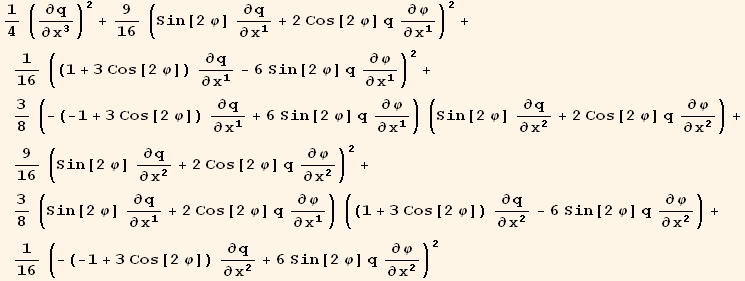

![( {{1/8 (5 + 3 Cos[2 φ]), 3/8 Sin[2 φ], 0}, {3/8 Sin[2 φ], 1/8 (5 - 3 Cos[2 φ]), 0}, {0, 0, 1/4}} )](HTMLFiles/index_234.gif)
![( {{-3/8 Sin[2 φ] q, 3/8 (-3 + Cos[2 φ]) q, 0}, {3/8 (3 + Cos[2 φ]) q, 3/8 Sin[2 φ] q, 0}, {0, 0, 0}} )](HTMLFiles/index_235.gif)
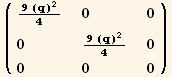



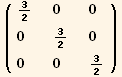
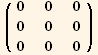
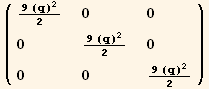

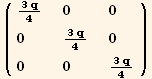
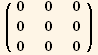
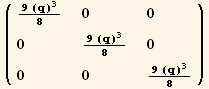
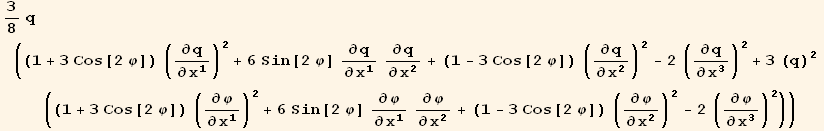

![( {{3/8 (1 + 3 Cos[2 φ]) q, 9/8 Sin[2 φ] q, 0}, {9/8 Sin[2 φ] q, 3/8 (1 - 3 Cos[2 φ]) q, 0}, {0, 0, -(3 q)/4}} )](HTMLFiles/index_293.gif)

![( {{9/8 (1 + 3 Cos[2 φ]) (q)^3, 27/8 Sin[2 φ] (q)^3, 0}, {27/8 Sin[2 φ] (q)^3, 9/8 (1 - 3 Cos[2 φ]) (q)^3, 0}, {0, 0, -(9 (q)^3)/4}} )](HTMLFiles/index_295.gif)
![ResultFrame[resLCI7 = (Qud[i, j] CovariantD[Qud[k, h], i]) (ContravariantD[(Qud[h, k]), j]) == 3/2 ∇q . Q . ∇q + 9q^2/2 ∇φ . Q . ∇φ]](HTMLFiles/index_300.gif)
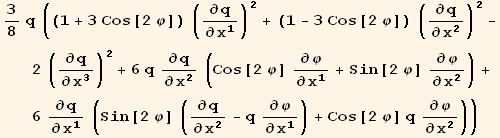

![( {{3/8 (1 + 3 Cos[2 φ]) q, 9/8 Sin[2 φ] q, 0}, {9/8 Sin[2 φ] q, 3/8 (1 - 3 Cos[2 φ]) q, 0}, {0, 0, -(3 q)/4}} )](HTMLFiles/index_315.gif)
![( {{-9/8 Sin[2 φ] (q)^2, 9/8 Cos[2 φ] (q)^2, 0}, {9/8 Cos[2 φ] (q)^2, 9/8 Sin[2 φ] (q)^2, 0}, {0, 0, 0}} )](HTMLFiles/index_316.gif)
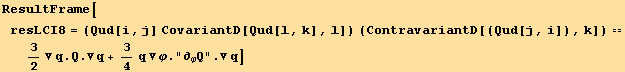
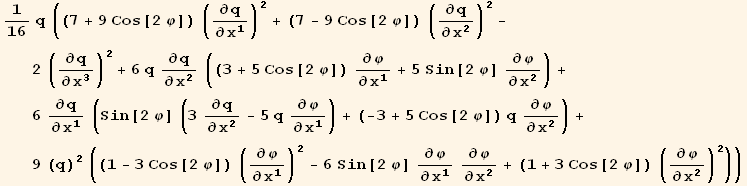

![( {{1/16 (7 + 9 Cos[2 φ]) q, 9/16 Sin[2 φ] q, 0}, {9/16 Sin[2 φ] q, 1/16 (7 - 9 Cos[2 φ]) q, 0}, {0, 0, -q/8}} )](HTMLFiles/index_337.gif)
![( {{-15/16 Sin[2 φ] (q)^2, 3/16 (-3 + 5 Cos[2 φ]) (q)^2, 0}, {3/16 (3 + 5 Cos[2 φ]) (q)^2, 15/16 Sin[2 φ] (q)^2, 0}, {0, 0, 0}} )](HTMLFiles/index_338.gif)
![( {{9/16 (1 - 3 Cos[2 φ]) (q)^3, -27/16 Sin[2 φ] (q)^3, 0}, {-27/16 Sin[2 φ] (q)^3, 9/16 (1 + 3 Cos[2 φ]) (q)^3, 0}, {0, 0, 0}} )](HTMLFiles/index_339.gif)

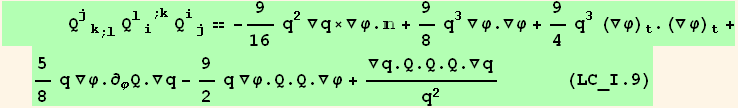
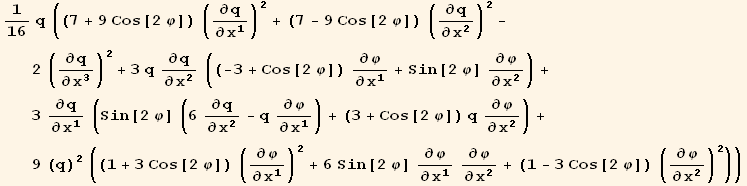

![( {{1/16 (7 + 9 Cos[2 φ]) q, 9/16 Sin[2 φ] q, 0}, {9/16 Sin[2 φ] q, 1/16 (7 - 9 Cos[2 φ]) q, 0}, {0, 0, -q/8}} )](HTMLFiles/index_363.gif)
![( {{-3/32 Sin[2 φ] (q)^2, 3/32 (3 + Cos[2 φ]) (q)^2, 0}, {3/32 (-3 + Cos[2 φ]) (q)^2, 3/32 Sin[2 φ] (q)^2, 0}, {0, 0, 0}} )](HTMLFiles/index_364.gif)
![( {{9/16 (1 + 3 Cos[2 φ]) (q)^3, 27/16 Sin[2 φ] (q)^3, 0}, {27/16 Sin[2 φ] (q)^3, 9/16 (1 - 3 Cos[2 φ]) (q)^3, 0}, {0, 0, 0}} )](HTMLFiles/index_365.gif)

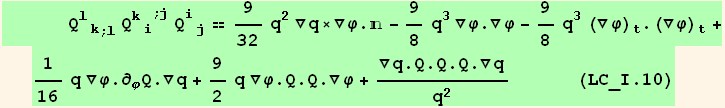
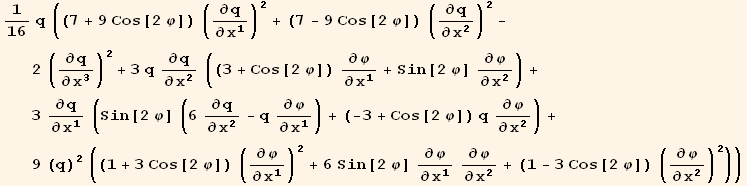

![( {{1/16 (7 + 9 Cos[2 φ]) q, 9/16 Sin[2 φ] q, 0}, {9/16 Sin[2 φ] q, 1/16 (7 - 9 Cos[2 φ]) q, 0}, {0, 0, -q/8}} )](HTMLFiles/index_387.gif)
![( {{-3/32 Sin[2 φ] (q)^2, 3/32 (-3 + Cos[2 φ]) (q)^2, 0}, {3/32 (3 + Cos[2 φ]) (q)^2, 3/32 Sin[2 φ] (q)^2, 0}, {0, 0, 0}} )](HTMLFiles/index_388.gif)
![( {{9/16 (1 + 3 Cos[2 φ]) (q)^3, 27/16 Sin[2 φ] (q)^3, 0}, {27/16 Sin[2 φ] (q)^3, 9/16 (1 - 3 Cos[2 φ]) (q)^3, 0}, {0, 0, 0}} )](HTMLFiles/index_389.gif)

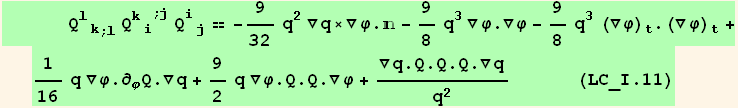
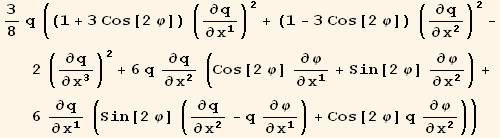

![( {{3/8 (1 + 3 Cos[2 φ]) q, 9/8 Sin[2 φ] q, 0}, {9/8 Sin[2 φ] q, 3/8 (1 - 3 Cos[2 φ]) q, 0}, {0, 0, -(3 q)/4}} )](HTMLFiles/index_411.gif)
![( {{-9/8 Sin[2 φ] (q)^2, 9/8 Cos[2 φ] (q)^2, 0}, {9/8 Cos[2 φ] (q)^2, 9/8 Sin[2 φ] (q)^2, 0}, {0, 0, 0}} )](HTMLFiles/index_412.gif)
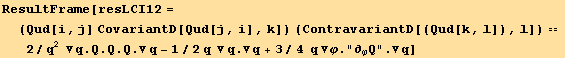

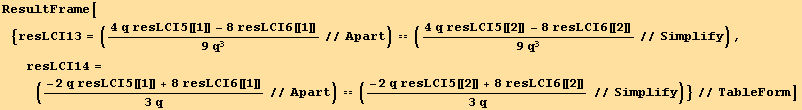

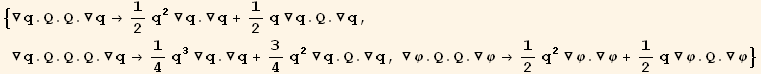

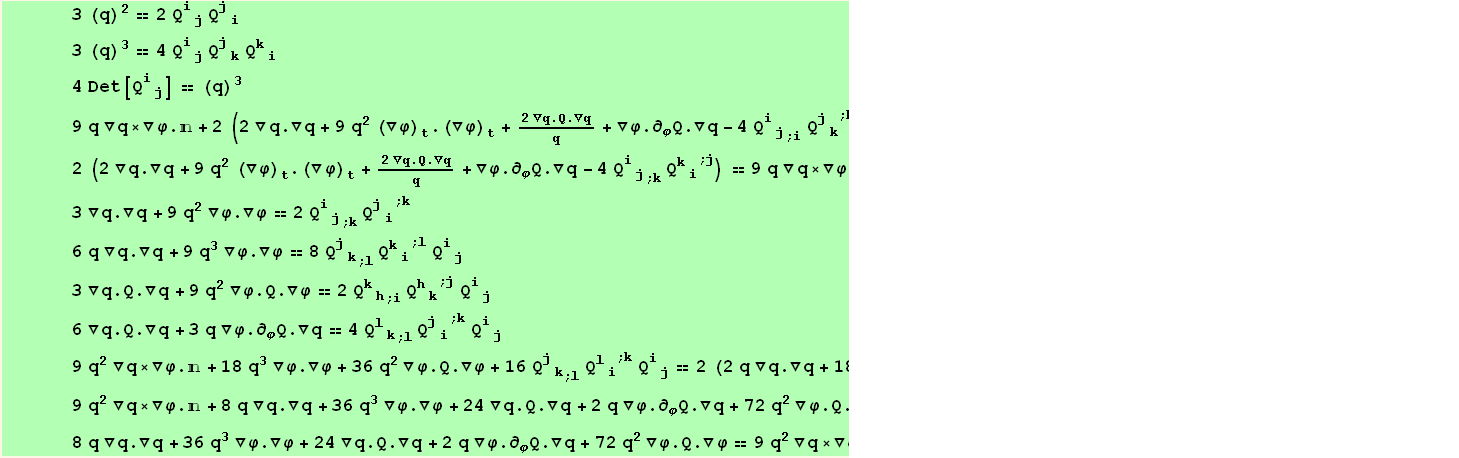



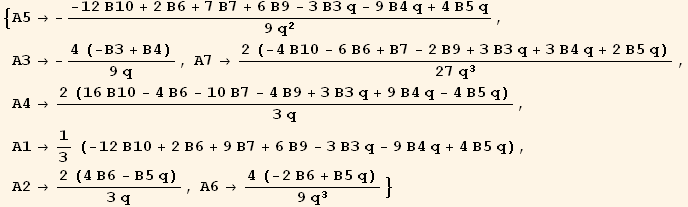
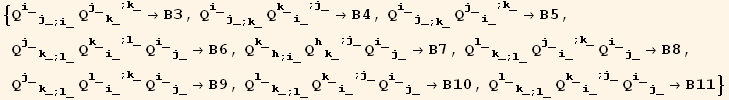
![ResultFrame[RES = {resLCI12[[1]] == resLCI8[[1]], Collect[4B11 - (4B10 - B3 q + B4 q), q, Factor] == 0, 2B8 - (4B10 - 2B6 - B7 + 2B9) == 0}/.BToQrule//TableForm]](HTMLFiles/index_453.gif)
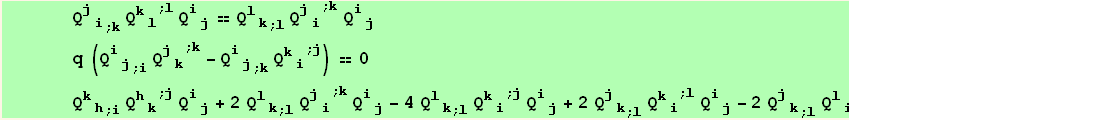

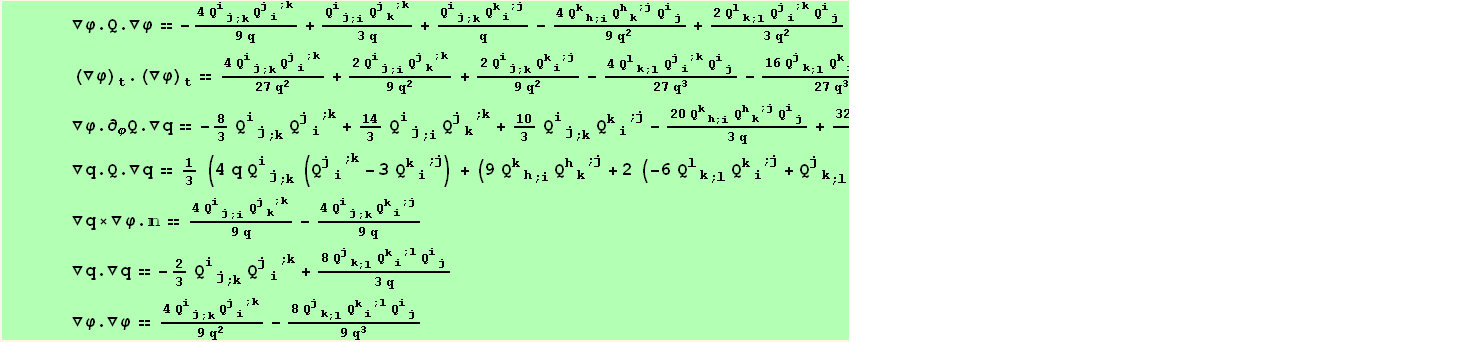
![fw[q] == δ[q]/3 + (2 δ[q]^2)/9 - (4 Δ[q])/3 (LC_I.18)](HTMLFiles/index_488.gif)
![gradgrad[p_, q_] = "grad[].grad[]" == (TGrad[, p][tu[q]] . TGrad[, r][td[q]]//EvaluateDotProducts[, g]//MetricSimplifyD[g])](HTMLFiles/index_493.gif)


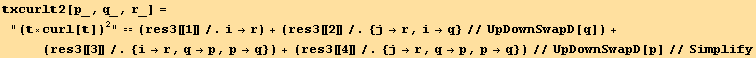
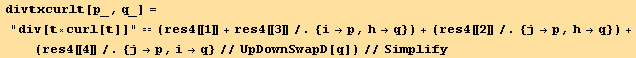
![res5 = (TGrad[, i][tu[p] td[p]] . TGrad[, q][tu[r] td[r]]//EvaluateDotProducts[, g]//MetricSimplifyD[g])/.i→q ;](HTMLFiles/index_507.gif)

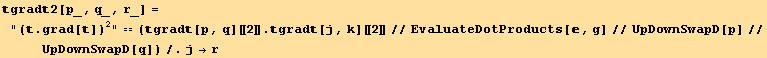

![listQa = Table[tu[p] td[i] CovariantD[tu[q], j] CovariantD[tu[r], k]/.Apply[Rule, Transpose[{{p, q, r}, Permutations[{i, j, k}][[n]]}], {1}], {n, 6}]//Sort](HTMLFiles/index_539.gif)

![listQu = (tu[i] td[i] Coefficient[res, tu[i] td[i]] + tu[j] td[i] Coefficient[res, tu[j] td[i]] + tu[j] td[i] (Coefficient[res, tu[k] td[i]]/.{k→j, j→k}))//Sort](HTMLFiles/index_550.gif)